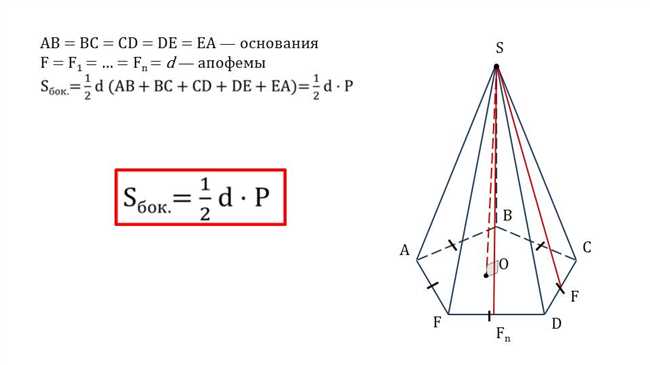
Если вы интересуетесь математикой, то, вероятно, слышали о понятии апофемы в правильной четырехугольной пирамиде. Апофема — это линия, которая соединяет вершину пирамиды с центром основания. На первый взгляд, может показаться, что нахождение апофемы в сложной геометрической фигуре будет трудной задачей. Однако, с помощью простого объяснения и формул, можно рассчитать ее без особых сложностей.
Для того, чтобы найти апофему, нужно знать высоту пирамиды и длину ребра основания. Используя формулу, можно получить точное значение апофемы, что позволит легко решать геометрические задачи, связанные с этим понятием.
Знание апофемы важно для понимания различных математических концепций и применения их на практике. Это одно из важных понятий, которое помогает углубиться в изучении геометрии и развить свои математические навыки. Поэтому, рассчитывая апофему в правильной четырехугольной пирамиде, вы сможете более полно и глубоко осознать эту науку и ее применение в реальном мире.
Определение апофемы в правильной четырехугольной пирамиде
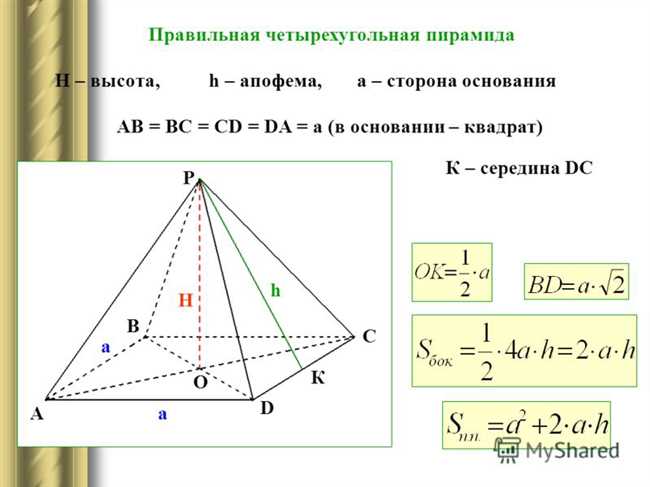
Для того чтобы найти апофему в правильной четырехугольной пирамиде, нужно знать следующие параметры:
- Длину ребра основания пирамиды, обозначим ее как «a»;
- Длину апофемы, обозначим ее как «b».
Используя данные параметры, можно найти апофему в правильной четырехугольной пирамиде с помощью формулы:
b = √(a² — (a/2)²)
где √(a² — (a/2)²) — это квадратный корень из разности квадрата длины ребра основания пирамиды и квадрата половины длины ребра основания.
Например, если известна длина ребра основания пирамиды «a» равная 8 см, то можно найти апофему пирамиды следующим образом:
b = √(8² — (8/2)²) = √(64 — 16) = √48 ≈ 6.93 см
Итак, апофема в данной пирамиде равна около 6.93 см.
Таким образом, апофема в правильной четырехугольной пирамиде может быть определена с использованием формулы, которая учитывает длину ребра основания пирамиды. Зная эту формулу, вы можете легко вычислить апофему пирамиды, которая служит как перпендикуляр и высота пирамиды одновременно.
Что такое апофема?
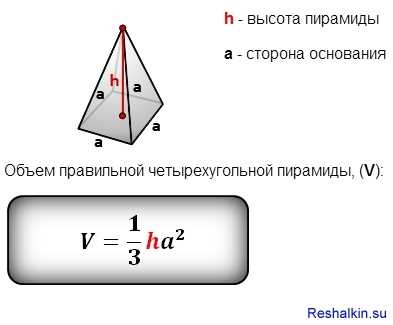
Чтобы лучше понять, что представляет собой апофема, давайте рассмотрим правильную четырехугольную пирамиду. Она состоит из основания в форме четырехугольника и четырех треугольных граней, которые сходятся в вершину пирамиды. Апофема же — это расстояние от вершины пирамиды до центра основания.
Апофема является важной характеристикой пирамиды, потому что она помогает определить ее размеры и свойства. Например, зная апофему и длины сторон основания, можно вычислить площадь основания и объем пирамиды. Это позволяет выполнять различные математические расчеты и применять понятие апофемы в различных задачах и областях науки.
Существует формула для вычисления апофемы пирамиды в зависимости от ее размеров. Для правильной четырехугольной пирамиды, апофема (a) может быть вычислена по формуле:
a = √(h^2 + (b/2)^2)
- a — апофема
- h — высота пирамиды
- b — сторона основания пирамиды
Используя эту формулу, можно легко вычислить апофему и получить необходимую информацию о пирамиде. Например, если известны высота пирамиды и длина стороны основания, можно легко вычислить апофему и использовать эту информацию для решения задачи или выполнять необходимые расчеты.
Таким образом, апофема является важным понятием в математике, которое помогает определить размеры и свойства объемных фигур, в том числе правильных четырехугольных пирамид. Зная апофему, можно выполнять различные математические расчеты и применять это понятие в практических задачах и исследованиях.
Определение четырехугольной пирамиды
Четырехугольная пирамида является одним из видов пирамид, и в зависимости от формы основания, она может быть разных типов: квадратная пирамида, прямоугольная пирамида, ромбовидная пирамида и т.д.
В квадратной четырехугольной пирамиде основание — это квадрат, а все грани, включая боковые и основание, образуют прямые углы. Такие пирамиды обладают симметрией по всем осям и являются основополагающими элементами во многих математических и геометрических концепциях.
Когда исследуем четырехугольную пирамиду, мы можем изучать ее параметры, такие как высота, образующая, углы и площадь поверхности. Для нахождения этих параметров существуют формулы, включая формулы для определения апофемы, которая является расстоянием от вершины пирамиды до середины основания. Апофема — это линия, которая является противоположной стороне основания в треугольнике, образующем грань пирамиды.
Важно помнить, что четырехугольная пирамида — это всего лишь одна из многих геометрических фигур, которые имеют свою уникальную структуру и свойства. Изучая их, мы можем расширить наше понимание математики и применить их в реальных ситуациях.
Как найти апофему в четырехугольной пирамиде?
Теперь давайте посмотрим, как можно найти апофему в четырехугольной пирамиде. Представим себе пирамиду с вершиной A и основанием в виде четырехугольника ABCD. Пусть M – середина ребра AB.
Шаг 1: Найдите длину ребра основания – отрезка AB. Для этого вам может потребоваться известная длина стороны основания. Например, если четырехугольник ABCD является квадратом со стороной a, то длина AB будет равна a.
Шаг 2: Найдите высоту пирамиды – отрезок AM. Высота пирамиды – это перпендикуляр, проведенный из вершины пирамиды на плоскость основания. Если вы знаете высоту пирамиды, то вам необходимо найти высоту треугольника AMB, который образуется основанием пирамиды и проведенным из вершины пирамиды до середины ребра основания.
Шаг 3: Используйте теорему Пифагора, чтобы найти апофему – отрезок OA. Для этого нужно сложить квадраты длины ребра основания и длины высоты пирамиды и извлечь из суммы квадратный корень: OA = √(AB² + AM²).
Вы также можете использовать другие формулы, если у вас есть другая информация о пирамиде, например, углы, стороны или диагонали основания.
Теперь вы знаете, как найти апофему в четырехугольной пирамиде. Попробуйте применить эти шаги к практическому примеру и проверьте свои навыки в решении геометрических задач!
Простое объяснение нахождения апофемы
Давайте сначала вспомним, что такое апофема. Апофема — это расстояние от вершины пирамиды до середины одной из ее боковых граней. Итак, как найти апофему? Для этого нам понадобятся некоторые формулы и математические понятия.
Шаг 1: Найдите высоту пирамиды
Первым шагом нам нужно найти высоту пирамиды. Высота пирамиды — это прямая линия из вершины пирамиды, перпендикулярная основанию. Как найти высоту пирамиды?
- Если у вас есть данные об основании пирамиды и угле между основанием и боковой гранью, можно воспользоваться тригонометрией. Например, для прямой четырехугольной пирамиды с квадратным основанием, формула будет такой: высота = сторона основания * косинус угла между основанием и боковой гранью.
- Если у вас есть данные о площади основания и объеме пирамиды, можно воспользоваться формулой объем = (площадь основания * высота) / 3. Из этой формулы можно выразить высоту пирамиды: высота = (объем * 3) / площадь основания.
Замечательно! Теперь, когда у нас есть высота пирамиды, мы можем перейти к следующему шагу.
Шаг 2: Найдите сторону треугольника на боковой грани
Вторым шагом нам понадобится найти сторону треугольника на боковой грани пирамиды. Как это сделать?
- Если у вас есть данные об основании пирамиды и одном из углов основания, можно воспользоваться теоремой косинусов. Например, для прямой четырехугольной пирамиды с квадратным основанием, формула будет такой: сторона треугольника = √ (сторона основания2 + сторона основания2 — 2 * сторона основания * сторона основания * косинус угла основания).
- Если у вас есть данные о боковой площади и периметре пирамиды, можно воспользоваться формулой площадь = (периметр боковой грани * сторона треугольника) / 2. Из этой формулы можно выразить сторону треугольника: сторона треугольника = (площадь * 2) / периметр боковой грани.
Ура! Теперь у нас есть сторона треугольника на боковой грани. Осталось последний шаг!
Шаг 3: Найдите апофему
Третьим и последним шагом мы найдем апофему пирамиды. Как это сделать?
- Апофема равна √ (высота2 + (сторона треугольника / 2)2).
Вот и все! Теперь вам известен способ нахождения апофемы в правильной четырехугольной пирамиде. Надеюсь, я смог объяснить этот процесс так, чтобы вы его поняли! Если у вас есть еще вопросы или нужна помощь с другими математическими понятиями, обращайтесь. Удачи в ваших математических приключениях!
Формула для вычисления апофемы
Апофема = √(полупериметр основания * высота пирамиды)
Для применения формулы необходимо знать полупериметр основания пирамиды и её высоту. Полупериметр основания вычисляется путем сложения длин всех четырех сторон основания и деления полученной суммы на 2. Высоту пирамиды можно измерить с помощью линейки или вычислить, зная другие характеристики пирамиды, такие как радиус описанной окружности.
Формула для вычисления апофемы является очень полезным инструментом при решении задач, связанных с пирамидами. Она позволяет быстро и точно определить длину апофемы, что может быть важно при рассмотрении различных свойств пирамиды или при решении практических задач из области архитектуры, геометрии и строительства.
