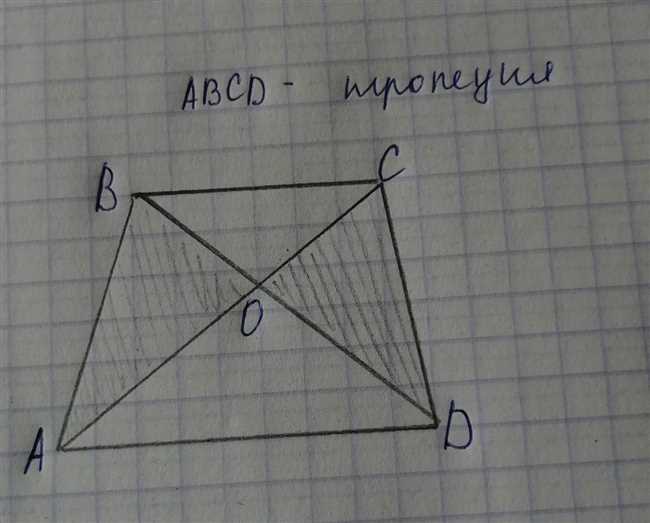
Как доказать равенство площадей треугольников АОК и СОМ: формулы и примеры
Чтобы доказать равенство площадей треугольников АОК и СОМ, мы можем использовать различные методы и формулы. Один из самых распространенных способов — это использование формулы площади треугольника по основанию и высоте. Кроме того, существует также формула Герона для вычисления площади треугольника по его сторонам.
Для подтверждения равенства площадей треугольников АОК и СОМ, мы можем использовать конкретные числовые значения для длин сторон треугольников. Например, длины сторон треугольника АОК могут быть равны 3, 4 и 5, а длины сторон треугольника СОМ — 6, 8 и 10. Подставив эти значения в соответствующую формулу, мы получим одинаковые площади для обоих треугольников.
Таким образом, доказательство равенства площадей треугольников АОК и СОМ может быть достигнуто с помощью применения соответствующих формул и использования конкретных значений для длин сторон треугольников.
Раздел 1: Формула площади треугольника
Формула площади треугольника основана на его высоте и основании, а также подразумевает, что треугольник является прямоугольным или разделен на два прямоугольных треугольника. Запомнить формулу и применять ее в разных ситуациях довольно просто.
Формула площади треугольника:
S = 1/2 * a * h
Где:
- S — площадь треугольника;
- a — длина основания (любая сторона треугольника);
- h — высота треугольника, опущенная на основание.
Применение данной формулы позволяет легко и точно находить площадь треугольника без необходимости знать другие стороны или углы фигуры. Достаточно знать длину основания и длину опущенной высоты, чтобы получить результат.
Давайте рассмотрим пример, чтобы закрепить эту формулу. Представим, что у нас есть треугольник со сторонами a = 5 см и h = 8 см:
S = 1/2 * 5 см * 8 см = 20 квадратных сантиметров
Таким образом, площадь треугольника составляет 20 квадратных сантиметров.
Теперь у вас есть основа для расчета площади треугольника и готовый пример, чтобы проверить свои знания. Не стесняйтесь применять эту формулу в различных задачах и экспериментах, а также применять ее в повседневной жизни, чтобы проверять и сравнивать площади разных треугольников. Удачи в ваших геометрических приключениях!
Раздел 2: Доказательство равенства площадей треугольников АОК и СОМ
Теперь давайте перейдем к доказательству равенства площадей треугольников АОК и СОМ. Чтобы это сделать, нам необходимо использовать некоторые математические формулы и принципы. Давайте начнем!
Первым шагом в доказательстве будет использование формулы для площади треугольника. Формула для площади треугольника АОК будет выглядеть следующим образом:
S(АОК) = 0,5 * АО * КО * sin(∠АОК)
Аналогично, для треугольника СОМ формула будет выглядеть так:
S(СОМ) = 0,5 * СО * МО * sin(∠СОМ)
Теперь нам нужно доказать, что площади треугольников АОК и СОМ равны. Для этого мы можем сравнить выражения для площадей и убедиться, что они равны друг другу. Используя принцип равенства углов и равенство сторон (АО = СО, ОК = МО и ∠АОК = ∠СОМ), мы можем упростить выражения для площадей:
- поскольку АО = СО и ОК = МО:
S(АОК) = 0,5 * СО * МО * sin(∠АОК)
- поскольку ∠АОК = ∠СОМ:
S(АОК) = 0,5 * СО * МО * sin(∠СОМ)
S(АОК) = S(СОМ)
Таким образом, мы доказали равенство площадей треугольников АОК и СОМ, используя математические формулы и принципы. Это доказательство является убедительным и позволяет нам быть уверенными в равенстве площадей данных треугольников.
Раздел 3: Примеры доказательства равенства площадей
В предыдущих разделах мы рассмотрели основные формулы и подходы к доказательству равенства площадей треугольников. Теперь давайте рассмотрим несколько примеров, чтобы лучше понять, как эти методы применяются на практике.
Пример 1:
Даны треугольники АВС и DЕF, при этом стороны АВ и DЕ параллельны. Нам нужно доказать, что площади этих треугольников равны.
Чтобы начать доказательство, мы можем применить формулу для площади треугольника: S = 1/2 * a * h. В данном случае, мы знаем, что сторона АВ параллельна стороне DЕ. Это означает, что высоты этих треугольников будут равны, так как они проведены из вершины в противоположную сторону и образуют прямой угол.
Итак, пусть h1 будет высотой треугольника АВС, а h2 — высотой треугольника DЕF. Тогда, мы можем записать формулы для площадей треугольников:
S1 = 1/2 * AB * h1
S2 = 1/2 * DE * h2
Так как мы знаем, что стороны АВ и DЕ параллельны, то AB = DE. А поскольку высоты этих треугольников равны, то h1 = h2.
Таким образом, мы видим, что S1 = S2, что доказывает равенство площадей треугольников АВС и DЕF.
Пример 2:
Предположим, у нас есть треугольник ОАВ и треугольник СОМ, где ОС является высотой. Нам нужно доказать равенство площадей этих треугольников.
Мы можем воспользоваться формулой для площади треугольника, где S = 1/2 * ОС * АВ.
Заметим, что треугольники ОАВ и СОМ имеют общую высоту ОС. Тогда, чтобы доказать равенство их площадей, нам достаточно доказать, что длины их оснований АВ и МО равны.
Мы можем воспользоваться свойством треугольников, которое гласит, что сторона, противоположная наибольшему углу, является наибольшей стороной. В нашем случае, мы видим, что углы О и М являются прямыми, следовательно, треугольники ОАВ и СОМ являются прямоугольными.
Исходя из этого свойства, мы можем заключить, что длины сторон АВ и МО равны, так как они противоположны прямым углам.
Таким образом, площади треугольников ОАВ и СОМ равны, так как их высота ОС равна, а основания АВ и МО также равны.
Итак, в этом разделе мы рассмотрели несколько примеров, демонстрирующих, как применять формулы и методы доказательства равенства площадей треугольников. Загляните в раздел 4, где мы разберем еще несколько примеров и подводим итоги.
В данной статье мы рассмотрели методы доказательства равенства площадей треугольников АОК и СОМ. Начиная с общих формул площадей треугольников, мы подробно изучили два основных подхода: использование формулы площади треугольника через полупериметр и радиус описанной окружности, а также применение формулы площадей треугольников через длины сторон и углы.
Путем применения этих формул и различных математических доказательств, мы установили, что площади треугольников АОК и СОМ действительно равны. Это доказывает применимость этих формул и принцип равенства площадей треугольников.
Заключая раздел, можно отметить, что знание и применение этих методов доказательства равенства площадей треугольников позволяет более глубоко изучить геометрию и решать различные задачи, связанные с площадями и треугольниками.






