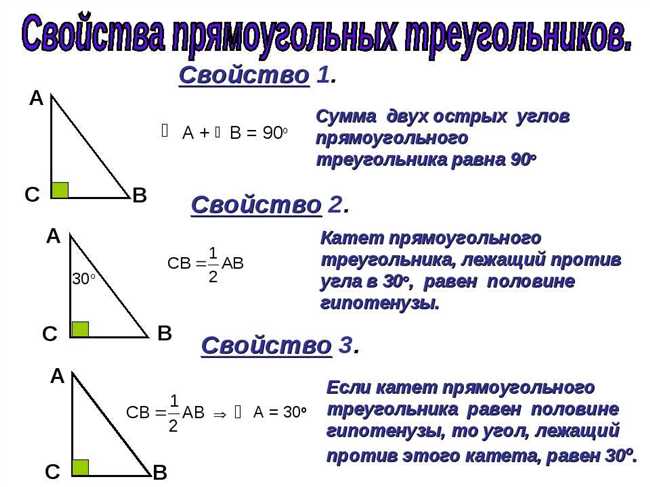
Гипотенуза — один из основных элементов геометрии, широко известный благодаря теореме Пифагора. Этот термин относится к прямоугольному треугольнику и обозначает его самую длинную сторону, которая находится напротив прямого угла.
Гипотенуза играет важную роль в геометрии и используется для вычисления других параметров треугольников, например, его площади и периметра. Также она является ключевым элементом в тригонометрии, где она используется в тригонометрических соотношениях и формулах.
Изучение гипотенузы и ее свойств позволяет нам лучше понять пространственные отношения и взаимодействие геометрических фигур, а также применять их в реальных ситуациях, например, при измерении расстояний или выполнении инженерных расчетов.
Что такое гипотенуза?
Этот термин происходит от греческого слова «hypoteinousa», которое означает «натянутая под». Это отражает геометрическое свойство гипотенузы — она является глобальной опорой треугольника, которая поддерживает остальные стороны вместе.
Определение гипотенузы важно в математике и физике, поскольку она позволяет нам решать различные задачи, связанные с прямоугольными треугольниками и их свойствами.
Итак, каким образом можно найти длину гипотенузы? Мы можем использовать известные длины катетов и применить теорему Пифагора. В этой теореме гипотенуза в квадрате равна сумме квадратов катетов. Формула выглядит следующим образом:
c^2 = a^2 + b^2
Где c — длина гипотенузы, а и b — длины катетов. Обратите внимание, что эта формула работает только для прямоугольных треугольников.
Применение теоремы Пифагора и понимание гипотенузы позволяют решать многочисленные задачи в геометрии, физике, инженерии и других областях. Например, мы можем использовать гипотенузу для вычисления площади треугольника, определения углов, нахождения расстояний в пространстве и многое другое.
Важно помнить, что гипотенуза — это больше, чем просто сторона треугольника. Она является ключевым элементом, который позволяет нам понять и решить широкий спектр задач и проблем. Так что не забывайте о гипотенузе, когда сталкиваетесь с прямоугольными треугольниками!
Как найти длину гипотенузы?
Итак, как найти длину гипотенузы? Ответ прост: используйте теорему Пифагора! Если вам заданы длины двух катетов в прямоугольном треугольнике, вы можете найти длину гипотенузы, применяя следующую формулу: гипотенуза в квадрате равна сумме квадратов катетов.
Теорема Пифагора стала одной из наиболее известных теорем в истории геометрии. Она сформулирована в виде простого уравнения, но ее влияние и применение огромны.
Позвольте мне привести пример, чтобы проиллюстрировать использование теоремы Пифагора. Представьте себе прямоугольный треугольник, где один катет равен 3, а другой катет равен 4. Вы хотите найти длину гипотенузы. Применяя теорему Пифагора, мы можем записать:
гипотенуза в квадрате = 3 в квадрате + 4 в квадрате
Вычислив, получим:
гипотенуза в квадрате = 9 + 16 = 25
Теперь возьмем квадратный корень от 25, чтобы найти длину гипотенузы:
гипотенуза = √25 = 5
Таким образом, длина гипотенузы в примере равна 5.
Используя теорему Пифагора, вы можете легко находить длину гипотенузы в других примерах. Относитесь к ней как к мощному инструменту, позволяющему решать разнообразные геометрические задачи.
Гипотенуза и теорема Пифагора
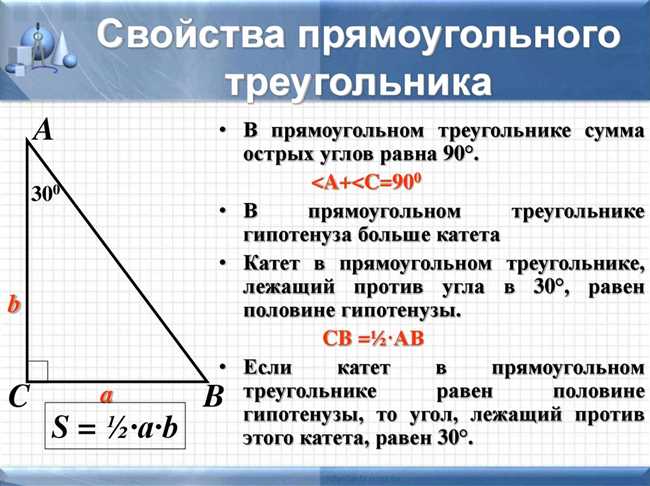
Гипотенуза — это понятие, которое мы используем в прямоугольном треугольнике. Прямоугольный треугольник — это треугольник, у которого один из углов равен 90 градусам. Гипотенуза — это наибольшая сторона треугольника, она противолежит прямому углу.
Теорема Пифагора, возможно, является одной из самых известных формул в математике. Она гласит следующее: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин его катетов.
Теперь представьте себе треугольник со сторонами a, b и c, где c — гипотенуза. По теореме Пифагора, у нас есть следующее равенство: c^2 = a^2 + b^2.
Так, если мы знаем длины двух сторон прямоугольного треугольника, мы можем найти длину его гипотенузы, просто подставив значения в формулу Пифагора и решив уравнение.
Давайте рассмотрим пример, чтобы понять, как применять теорему Пифагора. Представьте себе треугольник со сторонами 3 и 4. Мы хотим найти длину гипотенузы. Подставим значения в формулу: c^2 = 3^2 + 4^2, что в свою очередь означает c^2 = 9 + 16. После простых математических действий мы получаем c^2 = 25. Длина гипотенузы будет равна 5, так как 5^2 = 25.
Теорема Пифагора имеет множество практических применений в разных областях. Например, она широко используется в строительстве и архитектуре для вычисления длин сторон прямоугольных объектов, таких как двери и окна.
Теперь, когда вы знакомы с гипотенузой и теоремой Пифагора, вы можете увидеть, что эти понятия имеют важное значение в геометрии и в повседневной жизни. Они помогают нам понять и описать взаимосвязи между сторонами прямоугольного треугольника и применить их для различных расчетов.
Заключение: примеры гипотенузы в реальной жизни
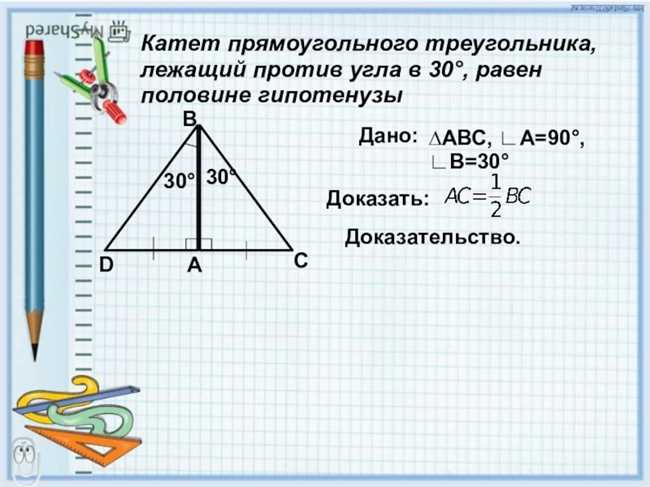
1. Конструкция домов и зданий
Гипотенуза применяется в строительстве для определения и расчета длины диагоналей прямоугольных стен и фундаментов. Это позволяет обеспечить стабильность и прочность конструкции, а также создать оптимальную комфортную среду для жизни и работы.
2. Медицинские исследования
В медицине гипотенуза применяется при обработке и анализе изображений, полученных с помощью медицинских сканеров и аппаратов. Например, при исследовании мозга, расстояние между различными точками на изображении может быть определено с использованием гипотенузы.
3. Навигация и геопозиционирование
Гипотенуза также используется в навигационных системах и GPS. При определении местоположения объекта на карте, где координаты X и Y представляют собой катеты прямоугольного треугольника, используется гипотенуза для расчета расстояния и определения точного положения.
Таким образом, гипотенуза является неотъемлемой частью различных областей нашей жизни, от строительства до медицины и навигации. Ее использование позволяет решать задачи эффективно и точно, обеспечивая нам комфорт и безопасность.






