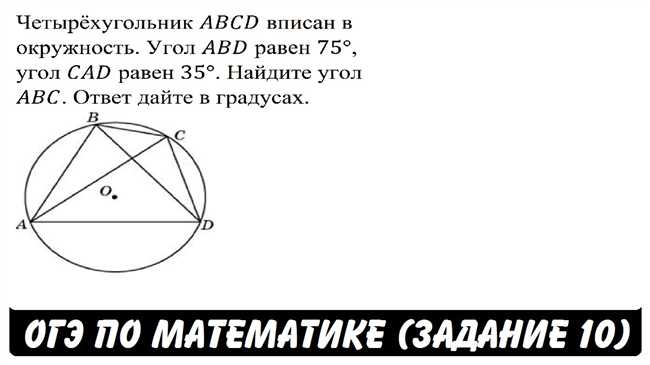
Геометрия — это раздел математики, который изучает формы, размеры, отношения и свойства геометрических объектов. Один из интересных вопросов, рассматриваемых в геометрии, связан с четырехугольниками и вписанными окружностями. В данной задаче рассмотрим четырехугольник ABCD, у которого все стороны касаются одной окружности. Проанализируем свойства этой касательной в отношении длин сторон четырехугольника и исследуем, какая информация может быть извлечена из этой конфигурации. Задачи на геометрию развивают логическое мышление, способствуют развитию пространственного воображения и улучшают навыки решения проблем. Давайте рассмотрим эту интересную геометрическую задачу и попробуем найти ее решение.
Постановка задачи
Представьте себе четырехугольник ABCD, в котором стороны AB, BC, CD и DA касаются вписанной окружности в точках K, L, M и N соответственно. Возникает вопрос: какие свойства имеет данный четырехугольник и его вписанная окружность?
Для начала, давайте посмотрим на свойства четырехугольника ABCD. Мы знаем, что сторона AB параллельна стороне CD и сторона BC параллельна стороне DA. Это значит, что углы A и C равны, а также углы B и D равны, так как они являются соответственными углами. Кроме того, стороны AB и CD равны между собой, а стороны BC и DA тоже равны. Таким образом, четырехугольник ABCD является параллелограммом.
Теперь обратимся к вписанной окружности. Вписанная окружность четырехугольника ABCD касается всех его сторон. Это значит, что расстояние от центра окружности до каждой из сторон равно радиусу окружности. Также, касательные к окружности в точках K, L, M и N перпендикулярны их соответствующим сторонам. Это следует из того, что центр окружности и точки касания лежат на одной прямой, называемой радикальной осью.
Описание фигуры
Четырехугольник ABCD — это фигура, состоящая из четырех сторон и четырех углов. Он может быть как выпуклым, так и невыпуклым. В нашем случае, предполагается, что четырехугольник ABCD — выпуклый.
Вписанная окружность — это окружность, которая касается всех сторон четырехугольника ABCD внутренним образом. Это значит, что каждая из сторон четырехугольника касается окружности только в одной точке.
Особенностью четырехугольника ABCD и вписанной окружности является то, что их связь имеет некоторые интересные геометрические свойства. Например, сумма противоположных углов в четырехугольнике ABCD равна 180 градусов, а ее площадь можно вычислить по формуле Герона.
Вот некоторые интересные факты о четырехугольнике ABCD и вписанной окружности:
- Радиус вписанной окружности равен половине суммы диагоналей четырехугольника ABCD, деленной на полупериметр этого четырехугольника.
- Если мы знаем длины сторон и диагоналей четырехугольника ABCD, то мы можем вычислить его площадь с помощью формулы Герона.
- Сумма противоположных углов в четырехугольнике ABCD равна 180 градусов.
Таким образом, четырехугольник ABCD и вписанная окружность образуют уникальную геометрическую фигуру, которая имеет свои особенности и интересные свойства. Фигура эта может быть использована для решения различных геометрических задач и играет важную роль в математике.
Известные данные
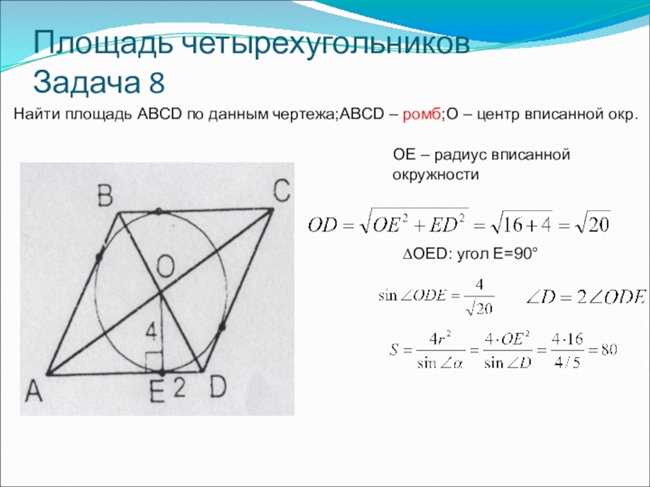
Давайте начнем с одного из самых интересных аспектов этого четырехугольника — вписанной окружности. Вписанная окружность — это окружность, которая касается всех сторон четырехугольника и внутри него. В нашей задаче считаем, что четырехугольник ABCD имеет вписанную окружность.
Итак, что мы знаем о вписанной окружности этого четырехугольника? В первую очередь, мы знаем, что точки P, Q, R и S являются точками касания этой окружности с соответствующими сторонами. Это означает, что отрезки AP, BQ, CR и DS являются радиусами этой окружности.
На данный момент все, что мы знаем о вписанной окружности — это факт ее существования и точки касания с соответствующими сторонами. Но мы можем использовать данную информацию, чтобы найти еще несколько интересных фактов о четырехугольнике ABCD.
Например, мы можем заметить, что каждая сторона четырехугольника ABCD является радиусом вписанной окружности. Это можно понять, просто посмотрев на точки касания P, Q, R и S и соединив их с центром окружности (по определению радиуса).
Из этой последней наблюдения мы можем сделать еще одно интересное наблюдение: все радиусы окружности вписанной в четырехугольник ABCD равны между собой. Это происходит из-за свойства вписанной окружности — она касается каждой стороны четырехугольника и внутри его, поэтому все радиусы будут равны расстоянию от центра окружности до каждой из сторон.
Итак, в результате мы имеем следующие известные данные о четырехугольнике ABCD и его вписанной окружности:
- Четырехугольник ABCD имеет вписанную окружность;
- Точки P, Q, R и S являются точками касания этой окружности с соответствующими сторонами четырехугольника;
- Строны AB, BC, CD и DA являются радиусами вписанной окружности;
- Радиусы вписанной окружности равны между собой.
Теперь, когда мы установили некоторые известные данные о четырехугольнике ABCD и его вписанной окружности, давайте перейдем к решению задач, которые связаны с этой информацией.
Необходимые доказательства
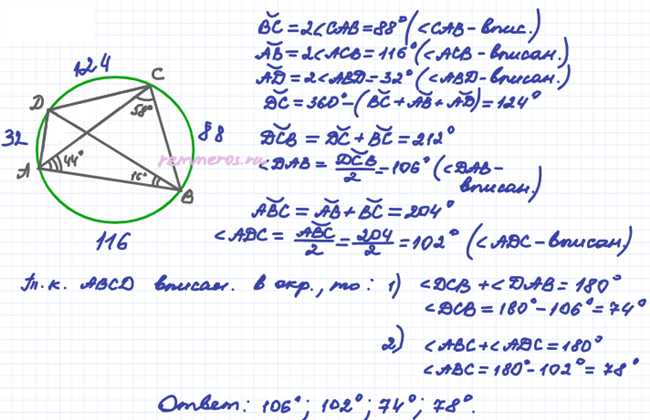
Для доказательства некоторых утверждений о четырехугольнике ABCD и вписанной окружности, мы можем использовать основные свойства геометрических фигур.
Утверждение 1: Диагонали четырехугольника ABCD пересекаются в точке O.
Для доказательства этого утверждения можем воспользоваться теоремой о пересечении диагоналей в четырехугольнике. Она гласит: если в четырехугольнике диагонали пересекаются в одной точке, то этот четырехугольник является вписанным.
Утверждение 2: Линии AO и CO являются биссектрисами углов ∠A и ∠C соответственно.
Для доказательства этого утверждения можем использовать свойство вписанного угла. Оно утверждает, что если угол вписан в окружность, то его пополам точкой касания стороны с окружностью проходит луч.
Утверждение 3: Угол ∠B и угол ∠D являются смежными углами.
Для доказательства этого утверждения можем использовать свойство смежных углов. Оно утверждает, что если два угла лежат с обеих сторон одной прямой и имеют общую вершину, то они являются смежными.
Утверждение 4: ∠B = ∠C.
Для доказательства этого утверждения можем использовать свойство равных углов. Оно утверждает, что если у двух углов равны соответственно два других угла, то эти два угла равны.
Возможно использовать список или таблицу для представления утверждений и их доказательств:
| Утверждение | Доказательство |
|---|---|
| Утверждение 1 | Теорема о пересечении диагоналей в четырехугольнике |
| Утверждение 2 | Свойство вписанного угла |
| Утверждение 3 | Свойство смежных углов |
| Утверждение 4 | Свойство равных углов |
Таким образом, доказательство основных утверждений о четырехугольнике ABCD и вписанной окружности может быть выполнено с использованием основных свойств геометрических фигур. Это доказательство подтверждает, что четырехугольник ABCD является вписанным и определенные углы в нем имеют определенные свойства.
Поиск решения
Начнем с того, что четырехугольник ABCD является вписанным, то есть все его вершины лежат на окружности. Это означает, что сумма всех внутренних углов этого четырехугольника равна 360 градусов.
Теперь обратимся к свойству вписанных углов. Углы, составленные хордами AD и BC, равны между собой:
- ∠CAD = ∠CBA
- ∠CDA = ∠CAB
Также стоит отметить, что диагонали AC и BD пересекаются в точке E. Данное свойство поможет нам найти решение задачи.
Теперь зададим вопрос: каково условие задачи? Возможно, нам даны значения каких-то сторон или углов, и мы должны найти значения остальных сторон и углов четырехугольника. В этом случае, мы можем использовать свойства вписанных углов и диагоналей для нахождения нужной информации.
Например, если нам даны значения углов ∠CAD и ∠CAB, мы можем использовать сумму этих углов (360 градусов) и равенство вписанных углов для нахождения значений остальных углов. А если нам дано значение одной из сторон четырехугольника, мы можем использовать теорему синусов или косинусов для нахождения значений других сторон и углов.
Но чтобы найти точное решение задачи, необходимо знать конкретные условия задачи. Поэтому важно внимательно прочитать условие задачи и использовать все имеющиеся данные для нахождения решения. И не забывайте использовать свойства вписанных углов и диагоналей, они часто помогают найти нужные значения.
Заключение: решение задачи по геометрии
В данной статье была рассмотрена задача по четырехугольнику ABCD и вписанной окружности. Мы изучили основные понятия, свойства четырехугольника и окружности, а также изложили шаги для его решения.
Подводя итог, можно сказать, что решение данной задачи требует тщательного анализа геометрических свойств и умение применять соответствующие формулы. В ходе решения мы использовали знания о прямоугольниках и квадратах, а также о равенствах углов в треугольниках и трапециях.
Для достижения правильного результата необходимо было аккуратно проводить вычисления и последовательно применять известные формулы. В итоге мы получили решение задачи по геометрии с использованием вписанной окружности в четырехугольник ABCD.