Формула cosinus x: простое объяснение и важные свойства

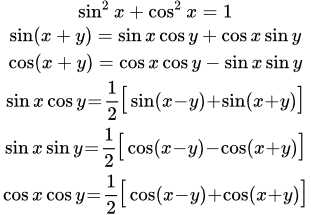
Формула cosinus x является одной из основных тригонометрических формул, которая позволяет найти значение косинуса угла x. Косинус — это отношение прилежащего катета к гипотенузе прямоугольного треугольника. Формула cosinus x можно выразить следующим образом: cos x = прилегающая сторона / гипотенуза. Важно отметить, что x должен быть выражен в радианах. Косинус имеет ряд важных свойств, таких как периодичность с периодом 2π, симметрию относительно оси ординат и значения, ограниченные в интервале [-1;1]. Зная значения угла x, можно с помощью формулы cosinus x вычислить его косинус и применять результаты в различных задачах и формулах.

Что такое cosinus x и как его вычислить?

Чтобы понять, как вычислить cosinus x, нам нужно разобраться в самой функции и ее свойствах. Cosinus x – это отношение, которое равно прилежащей стороне прямоугольного треугольника, деленной на гипотенузу. Значение cosinus x может быть от -1 до 1, и оно зависит от величины угла x. Когда угол x равен 0 градусов, cosinus x равен 1. Когда угол x равен 90 градусов, cosinus x равен 0. Когда угол x равен 180 градусов, cosinus x равен -1.

К счастью, чтобы вычислить значение cosinus x, нам не нужно находить прилежащую сторону и гипотенузу каждый раз. Существуют таблицы и графики, которые дают нам значения cosinus для всех углов от 0 до 360 градусов. Мы можем использовать эти таблицы, чтобы найти значение cosinus x в зависимости от заданного угла x.

Кроме таблиц, существуют также математические функции и калькуляторы, которые могут вычислить значение cosinus x из любого указанного угла. Например, на большинстве наших научных калькуляторов есть кнопка cos, которую мы можем использовать для вычисления cosinus x.

Также есть математическая формула для вычисления cosinus x, называемая рядом Тейлора. Этот ряд представляет собой бесконечную сумму, которая сходится к значению cosinus x с определенной точностью. Однако эта формула может быть сложной для понимания и вычисления вручную, поэтому использование таблиц или калькуляторов может быть более удобным и быстрым вариантом для обычного пользователя.

Свойства функции cosinus x и его важные особенности

1. Периодичность:

Одной из основных особенностей функции cos x является ее периодичность. Функция cos x повторяется через каждые 2π радиан или 360 градусов. Это означает, что значения функции в точках x и x+2π радиан (или x+360 градусов) будут совпадать. Например, cos 0 равен 1, и cos 2π также равен 1.

2. Значения на интервале:

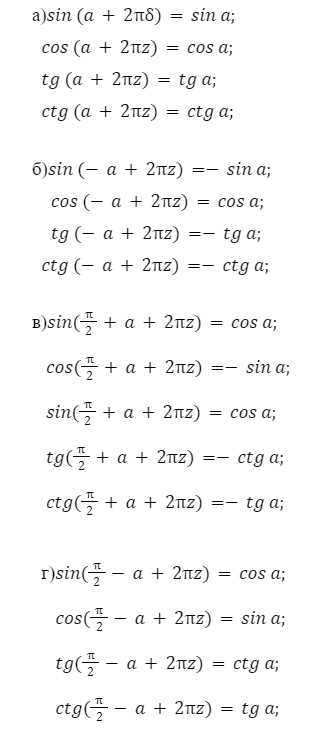
Значение функции cos x изменяется в пределах от -1 до 1 на всем числовом интервале. Максимальное значение равно 1, когда x равен 0, а минимальное значение -1, когда x равен π радиан или 180 градусов. Функция cos x также принимает все возможные значения между -1 и 1 в пределах периода.

3. Симметрия:

Функция cos x обладает осевой симметрией относительно оси ординат (ось y). Это означает, что значения функции симметричны относительно точки (0, 0). Например, cos (-x) равен cos x для любого значения x.

4. Гармонические колебания:

Функция cos x представляет собой гармоническое колебание, которое повторяется через равные промежутки времени или угла. Гармонические колебания играют важную роль в физике, инженерии и других науках, так как многие физические явления можно описать с помощью этой функции.

5. Другие свойства:

• Функция cos x является четной функцией, что означает, что cos (-x) = cos x для любого значения x.
• Между функциями cos x и sin x существует тождественное соотношение, известное как тригонометрическая идентичность: cos^2 x + sin^2 x = 1.
• Функция cos x имеет множество приложений в физике, математике, инженерии, компьютерной графике и других областях.

Надеюсь, эта информация помогла вам лучше понять свойства функции cosinus x и его важные особенности. Если у вас остались вопросы или есть что добавить, не стесняйтесь задавать и делиться своими мыслями!

Применение cosinus x в математике и естественных науках

1. Геометрия

В геометрии cosinus x часто используется для нахождения длины сторон треугольника и измерения углов. Например, с помощью теоремы косинусов можно найти длину третьей стороны треугольника, если известны длины двух других сторон и угол между ними. Также cosinus x используется для определения проекций векторов и расчета расстояний между точками в трехмерном пространстве.

2. Физика

В физике cosinus x применяется для описания гармонических колебаний и вращательных движений. Например, при анализе колебаний маятника или колебаний мембраны в акустике, cosinus x используется для определения амплитуды и фазы колебаний. В механике cosinus x применяется для определения силы или момента силы, действующего на объект под некоторым углом.

3. Инженерия

В инженерии cosinus x широко используется при проектировании и анализе различных систем. Например, при расчете напряжения в статических конструкциях, cosinus x помогает определить силу, действующую на элемент под определенным углом. Также cosinus x используется в электротехнике при расчете фазовых сдвигов в электрических цепях.

4. Медицина

В медицине cosinus x применяется для измерения углов и нахождения связи между различными переменными в осязаемой геометрии человеческого тела. Например, при изучении спрямляемых каналов кровеносной системы или при определении углов суставов при измерении гибкости суставного аппарата.

5. Космология

В космологии cosinus x применяется для измерения углов, например, при изучении углового размера космических объектов или при определении времени поворота звезды. Cosinus x также используется для анализа данных, полученных от космических телескопов и для определения орбитальных параметров астрономических объектов.

График функции cosinus x и его особенности

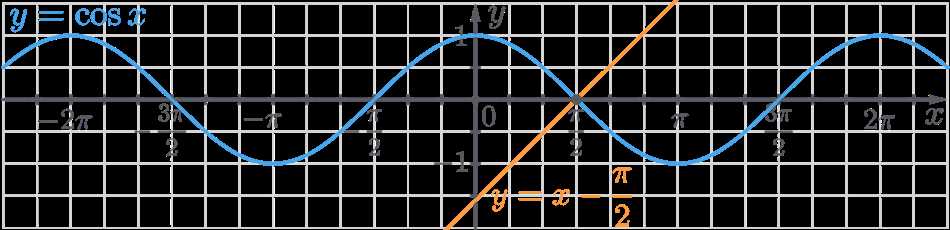
Если вы когда-либо наблюдали график функции cosinus x, то наверняка были поражены его красотой и симметрией. График cosinus x имеет множество интересных особенностей, которые мы сейчас рассмотрим.

Во-первых, график функции cosinus x представляет собой периодическую кривую, которая повторяется через каждые 2π радиан. Это означает, что значение cosinus x в точке x равно значению cosinus x в точке x+2π. Таким образом, график функции cosinus x можно рассматривать как бесконечно повторяющуюся кривую, которая продолжается как вправо, так и влево.

Другая особенность графика cosinus x — его ограниченность. Максимальное значение функции cosinus x равно 1, а минимальное значение -1. Это означает, что график функции cosinus x всегда ограничен между значениями 1 и -1 по оси y. Никакая точка на графике не может выходить за эти пределы.

График функции cosinus x также обладает особенностью пересечения оси y в точке (0, 1). Это означает, что при x=0 значение cosinus x равно 1. Данное пересечение оси y является характеристикой функции cosinus x и используется для определения ее периодичности.

Еще одна важная особенность графика cosinus x — его симметрия относительно оси y. Если отразить график функции cosinus x относительно оси y, то мы получим точно такой же график, только зеркально отраженный. Это означает, что значение функции cosinus x для отрицательного значения x равно значению функции cosinus x для положительного значения x с тем же модулем, но с противоположным знаком.

Наконец, график функции cosinus x имеет бесконечно много точек перегиба. Точка перегиба — это точка на графике, где кривая меняет свое направление из выпуклости вверх в выпуклость вниз или наоборот. График функции cosinus x имеет точки перегиба во всех целочисленных значениях x: …, -2π, -π, 0, π, 2π, … Именно в этих точках график функции cosinus x меняет свое направление и переходит от выпуклости вверх к выпуклости вниз или наоборот.

Такие особенности графика функции cosinus x делают его не только интересным для изучения, но и важным во многих областях науки и техники. Например, функция cosinus x широко применяется в физике, инженерии, математике и даже в музыке для описания колебательных процессов, сигналов и звуковых волн.

Практические примеры использования формулы cosinus x

Формула cosinus x имеет широкое применение в различных областях науки и техники. Вот несколько примеров, где она может использоваться:

• Механика и физика: Формула cosinus x может быть использована для определения угла наклона или направления движения объекта в пространстве. Также она может быть применена для расчета силы или компонентов силы, действующих на объект.
• Математика: Формула cosinus x используется в тригонометрии для нахождения значений угла или длины стороны треугольника на основе известных данных.
• Компьютерная графика и анимация: Формула cosinus x может быть использована для создания реалистичных движений объектов, изменения их ориентации и освещения.
• Статистика и вероятность: Формула cosinus x может быть применена для анализа данных и нахождения зависимостей между различными переменными.
• Электрическая и электронная инженерия: Формула cosinus x может быть использована для расчета фазового сдвига в электрических цепях или для определения значения переменного напряжения или тока.

Это лишь некоторые примеры использования формулы cosinus x, и она продолжает находить применение во многих других областях науки и техники. Понимание и применение этой формулы может значительно облегчить решение математических и физических задач, а также помочь в создании инновационных и эффективных решений в различных сферах.