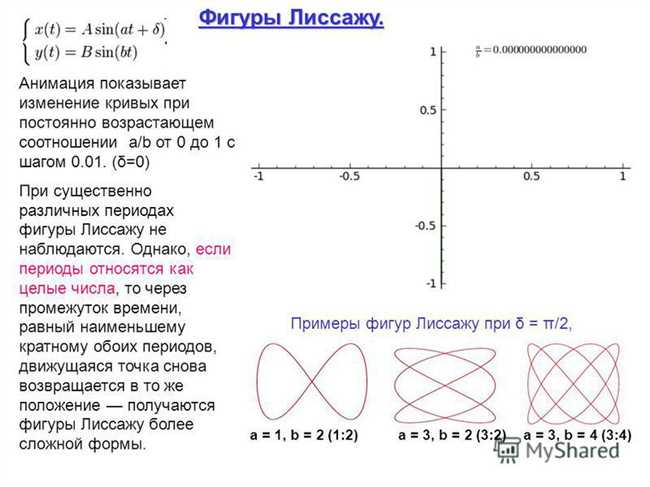
Фигуры Лиссажу – это особые геометрические фигуры, которые образуются при суперпозиции двух или более гармонических колебаний. Такая суперпозиция может быть представлена в виде графика или кривой, которая повторяет себя через равные временные интервалы. Названы эти фигуры в честь французского физика Жюля Лиссажу, который в 1850-х годах впервые изучал их свойства. Интересно, что форма фигур Лиссажу зависит от соотношения частот и фаз колебаний и может быть разнообразной, включая простые линии, эллипсы, круги и сложные многогранники. Фигуры Лиссажу широко используются в научных исследованиях, а также в искусстве и музыке для создания удивительных визуальных эффектов и зрительных образов.
Определение фигур Лиссажу
Для получения фигур Лиссажу используется два колебания – гармоническое колебание по горизонтали (x-координата) и гармоническое колебание по вертикали (y-координата). Эти колебания задаются с различными амплитудами, частотами и начальными фазами.
Когда два колебания пересекаются, точка перемещается по экрану и оставляет за собой след в виде графической кривой. Эта кривая представляет собой фигуру Лиссажу. Форма и характеристики фигуры Лиссажу зависят от соотношений амплитуд, частот и начальных фаз колебаний.
Фигуры Лиссажу имеют разнообразные формы, от простых эллипсов и окружностей до сложных многоугольников и кривых. Их особенностью является симметричность и регулярность, что делает их очень привлекательными для визуального представления и исследования.
Применение фигур Лиссажу включает множество областей, таких как физика, математика, акустика, электроника и искусство. Например, фигуры Лиссажу используются для визуализации фазовых портретов систем, сравнения частот и амплитуд волн, создания красивых паттернов на световых инсталляциях и многое другое. Они также широко используются в научных и учебных целях для демонстрации принципов колебаний и волн.
Математические основы фигур Лиссажу
Основой для формирования фигур Лиссажу служат гармонические колебания, которые можно представить в виде синусоидальных функций. Как мы знаем, синусоида — это график, который описывает периодическое поведение, например, движение колеблющегося тела или электрический сигнал.
Возьмем два гармонических колебания с разными частотами и построим их графики на плоскости. Один график будет представлять собой колебание по горизонтали (по оси Х) и будет выражен в синусоидальной форме, а другой график будет представлять колебание по вертикали (по оси Y) и будет выражен в косинусоидальной форме. При совместном движении этих колебаний на плоскости будут получаться фигуры Лиссажу.
Значение каждой координаты точки на графике определяется значениями амплитуд и фаз обеих колебаний в данной точке времени. Таким образом, при разных частотах и фазах колебаний, мы получаем разнообразные формы фигур Лиссажу.
Интересно, что фигуры Лиссажу могут быть использованы для визуализации различных физических явлений, например, для определения частоты и фазы колебаний или для настройки электронных приборов. Они также могут использоваться в искусстве и дизайне, добавляя уникальность и красоту визуальным композициям.
Примеры фигур Лиссажу

Фигуры Лиссажу представляют собой графическую интерпретацию зависимости между двумя гармоническими колебаниями. Они могут быть представлены в виде кривых на плоскости или через различные устройства, такие как осциллографы.
Приведу несколько примеров фигур Лиссажу:
- Пример 1: Фигура Лиссажу с отношением частот 1:1
- Пример 2: Фигура Лиссажу с отношением частот 2:1
- Пример 3: Фигура Лиссажу с отношением частот 3:2
- Пример 4: Фигура Лиссажу с несимметричной формой
Если частота колебаний по горизонтальной оси равна частоте колебаний по вертикальной оси, то фигура Лиссажу будет представлять собой эллипс. Этот пример демонстрирует простую гармоническую зависимость и позволяет наглядно увидеть синхронизацию двух колебаний.
Если частота колебаний по горизонтальной оси вдвое выше частоты колебаний по вертикальной оси, то фигура Лиссажу будет иметь форму эллипса, похожую на горизонтальную оваль. Этот пример показывает, как изменение отношения частот влияет на форму фигуры Лиссажу.
В случае, когда отношение частот равно 3:2, фигура Лиссажу будет иметь форму круга. Этот пример показывает, что при определенных отношениях частот фигуры Лиссажу могут иметь необычные формы и структуры.
Фигуры Лиссажу могут иметь различные формы, включая несимметричные и сложные структуры. Например, если фазы колебаний по горизонтальной и вертикальной осям не совпадают, то форма фигуры Лиссажу будет сложнее и будет иметь более запутанную структуру.
Это лишь небольшая подборка примеров фигур Лиссажу, которые могут быть созданы при различных отношениях частот и фаз колебаний. Каждая фигура Лиссажу представляет уникальную комбинацию колебаний и может служить испытанием для наших математических и эстетических суждений.
Применение фигур Лиссажу
Фигуры Лиссажу, полученные в результате модуляции сигналов, имеют множество практических применений в различных областях науки и техники. Давайте рассмотрим несколько интересных областей, в которых они используются.
1. Визуализация и анализ сигналов
Фигуры Лиссажу позволяют визуализировать и анализировать сигналы с помощью графиков. Например, если имеется два сигнала, например, сигналы синуса и косинуса, их можно модулировать друг на друга, чтобы получить фигуру Лиссажу. Такой график позволяет проанализировать фазовые и амплитудные характеристики этих сигналов.
Примером практического применения является анализ электрических сигналов в электротехнических системах. Фигуры Лиссажу широко используются для определения фазовых отклонений, проверки согласованности различных систем и выявления проблем, связанных с частотой и амплитудой сигналов.
2. Генерация звуковых эффектов
Фигуры Лиссажу также находят применение в области звуковых эффектов. Путем модуляции звукового сигнала можно создавать различные интересные звуковые эффекты, такие как хорусы, фазовые сдвиги, эхо и т. д. Для этого используется комбинация различных сигналов, которые создают сложные визуальные и звуковые фигуры Лиссажу.
3. Обучение и исследования
Фигуры Лиссажу также используются в области обучения и исследования. Они могут быть использованы в качестве визуального моделирования различных физических явлений, таких как колебания, интерференция и резонанс. Такие визуализации помогают студентам лучше понять и представить эти явления.
Кроме того, фигуры Лиссажу используются в научных исследованиях для изучения сложных колебательных процессов, таких как процессы в атомной, молекулярной и ядерной физике. Их анализ и исследование помогают получить новые знания и улучшить наше понимание фундаментальных принципов природы.
В общем, применение фигур Лиссажу распространено в различных областях науки и техники, от электроники и физики до музыки и зрелищных эффектов. Это мощный инструмент для визуализации и анализа сложных сигналов и исследования различных физических явлений. Вы можете начать экспериментировать с фигурами Лиссажу и применять их в своей работе или учебе!
Разновидности фигур Лиссажу

Разновидности фигур Лиссажу
Существует множество разновидностей фигур Лиссажу, которые могут быть созданы в зависимости от параметров гармонических колебаний. Основные разновидности фигур Лиссажу можно классифицировать по следующим параметрам:
- Отношение частот гармонических колебаний. Различное отношение частот приводит к формированию различных фигур, таких как эллипсы, окружности, гиперболы, прямые линии и т. д.
- Фазовый сдвиг между гармоническими колебаниями. Фазовый сдвиг может приводить к изменению формы фигуры Лиссажу и ее ориентации относительно осей координат.
- Амплитуда гармонических колебаний. Изменение амплитуды может приводить к изменению размера фигуры Лиссажу, ее искажению и деформации.
Комбинация указанных параметров и их вариаций позволяет получить неограниченное множество различных фигур Лиссажу. Возможности формирования и визуализации таких фигур используются в науке, технике, музыке и других областях. Фигуры Лиссажу привлекают внимание своей гармоничностью и красотой, а также являются важным инструментом для изучения и анализа гармонических колебаний и волновых процессов.






