- Геометрические свойства прямоугольника
- Определение прямоугольника
- Геометрические свойства сторон и углов прямоугольника
- Свойства сторон прямоугольника:
- Свойства углов прямоугольника:
- Свойства диагоналей прямоугольника
- Определение диагоналей прямоугольника
- Взаимное положение диагоналей
- Постановка задачи
- Доказательство равенства диагоналей прямоугольника

Равенство диагоналей в прямоугольнике может быть доказано несколькими способами. Одним из простейших и наиболее понятных является использование свойств прямоугольника. Возьмем, например, прямоугольник ABCD, где AB и CD — его стороны, AD и BC — его диагонали. Для начала построим соответствующие отрезки: AC и BD. Затем по ранее установленному свойству прямоугольника мы знаем, что его противоположные стороны равны по длине: AB = CD и AD = BC. Пользуясь этим фактом, у нас есть теперь два треугольника ADC и BAC, у которых стороны одного равны сторонам другого. Следовательно, эти треугольники являются равнобедренными. Что следует из этих равенств? Правильно, что их диагонали AD и BC тоже равны по длине. Таким образом, доказано, что диагонали прямоугольника равны друг другу.
Геометрические свойства прямоугольника

1. Равенство диагоналей
Начнем с самого известного свойства прямоугольника. Оно заключается в том, что длина диагонали прямоугольника равна и является главной диагональю. Это свойство можно доказать с помощью различных методов, например, используя теорему Пифагора или рассмотрев подобные треугольники.
2. Перпендикулярность сторон
Все четыре стороны прямоугольника перпендикулярны друг другу. Это значит, что каждая сторона прямоугольника образует прямой угол с каждой из соседних сторон. Такая геометрическая особенность позволяет легко распознавать прямоугольник и использовать его в конструировании.
3. Средняя линия
Средняя линия прямоугольника – это отрезок, соединяющий середины противоположных сторон. Он проходит через центр прямоугольника и является перпендикуляром к диагонали. Средняя линия равна половине длины диагонали и делит прямоугольник на два равных треугольника.
4. Центральная симметрия
Прямоугольник обладает центральной симметрией. Это значит, что если провести прямую, проходящую через его центр и перпендикулярную одной из сторон, то все точки, симметричные относительно этой прямой, будут находиться на другой стороне.
5. Площадь и периметр
Два важных параметра прямоугольника – его площадь и периметр. Площадь прямоугольника равна произведению длины одной из его сторон на длину соседней стороны. Периметр прямоугольника – это сумма длин всех его сторон.
6. Отношения длин сторон
Прямоугольник также обладает интересным свойством отношения длин его сторон. Если одна сторона прямоугольника в 1,5 раза длиннее другой, то кратные отношения сторон могут быть следующими: 2:3, 4:6, 6:9, и так далее.
| Отношение сторон | Длина одной стороны | Длина другой стороны |
|---|---|---|
| 2:3 | 2 | 3 |
| 4:6 | 4 | 6 |
| 6:9 | 6 | 9 |
Такие отношения сторон обусловлены тем, что у прямоугольника сохраняется пропорциональность его сторон при любом увеличении или уменьшении.
Вот такие важные геометрические свойства прямоугольника. Они помогают нам понять его особенности и решать задачи, связанные с этой фигурой. Теперь вы можете с легкостью утверждать, что прямоугольник – это гораздо больше, чем просто четырехугольник с прямыми углами и равными сторонами.
Определение прямоугольника
Прямоугольник можно представить как четырехугольник, у которого противоположные стороны параллельны и каждая пара противоположных сторон равна по длине. Это делает прямоугольник особым видом параллелограмма.
Прямоугольник можно описать с помощью его свойств:
- Углы: Углы прямоугольника равны 90 градусов каждый. Это означает, что противоположные углы прямоугольника также равны друг другу.
- Стороны: Прямоугольник имеет две параллельные противоположные стороны, каждая из которых равна по длине.
- Диагонали: Диагонали прямоугольника являются его особенностью. Длина каждой диагонали равна другой диагонали и образует равные треугольники с боковыми сторонами прямоугольника.
Прямоугольники обладают множеством практических применений в нашей повседневной жизни. Они используются в строительстве, архитектуре, дизайне интерьеров, изготовлении мебели и многих других областях. Их ровные углы и параллельные стороны делают их удобными для работы и измерений.
Геометрические свойства сторон и углов прямоугольника
Свойства сторон прямоугольника:
- Равность: стороны прямоугольника парные и равны между собой. Это означает, что противоположные стороны имеют одинаковую длину.
- Перпендикулярность: противоположные стороны прямоугольника пересекаются под прямым углом. Данное свойство позволяет прямоугольнику иметь прямые углы, которые являются основой для решения множества геометрических и физических задач.
Свойства углов прямоугольника:
- Прямой угол: все углы прямоугольника являются прямыми углами, то есть равны 90 градусам. Прямой угол — это угол, который образуется между двумя перпендикулярными линиями.
- Сумма углов: сумма углов в прямоугольнике равна 360 градусов. Это свойство следует из того, что в прямоугольнике есть 4 прямых угла.
Прямоугольник имеет также другие важные геометрические свойства:
- Диагонали: диагонали прямоугольника равны по длине и половинах разрезают друг друга. Это означает, что они делят прямоугольник на 4 равных треугольника. Доказательство равенства диагоналей прямоугольника может быть выполнено с использованием геометрических преобразований и свойств треугольников.
- Центральная симметрия: прямоугольник обладает центральной симметрией, что означает, что он может быть нанесен на себя симметрично относительно некоторой точки, называемой центром симметрии. В прямоугольнике центр симметрии является точкой пересечения его диагоналей.
Таким образом, стороны и углы прямоугольника обладают рядом важных свойств, которые широко используются в геометрии и других науках. Понимание этих свойств помогает в решении задач, связанных с этой фигурой, и создает основу для дальнейшего изучения геометрии.
Свойства диагоналей прямоугольника
1. Равенство длин: Одно из самых основных свойств диагоналей прямоугольника заключается в том, что они равны между собой. То есть, длина одной диагонали равна длине другой диагонали. Это легко понять, если вспомнить, что прямоугольник имеет равные стороны и противоположные углы.
2. Середина: Каждая диагональ делит прямоугольник на два равных треугольника. Более того, точка пересечения диагоналей является серединой каждой из диагоналей и разделяет их на две равные части. Таким образом, середина диагонали прямоугольника также является серединой каждой из сторон фигуры.
3. Перпендикулярность: Диагонали прямоугольника являются перпендикулярными. Это означает, что они образуют прямой угол при пересечении. Это утверждение может быть доказано с помощью свойства о параллельных сторонах прямоугольника.
4. Дважды длиннее медиан: Длина каждой диагонали прямоугольника в два раза больше длины медианы, проведенной из одной из вершин прямоугольника к середине противоположной стороны. Это можно видеть, если представить прямоугольник как состоящий из двух равных треугольников.
5. Площадь и длина: Иногда при решении задач связанных с прямоугольником, необходимо использовать связь между длиной диагоналей и площадью фигуры. Например, площадь прямоугольника можно выразить через длины его сторон и диагоналей, используя формулу S = p * q / 2, где S — площадь, p и q — длины сторон, а / — символ обозначает умножение.
Таким образом, диагонали прямоугольника имеют ряд важных свойств, которые помогают лучше понять и использовать эту фигуру. Они равны между собой, разделяют прямоугольник на равные части, перпендикулярны друг другу и связаны с длинами сторон и площадью прямоугольника.
Определение диагоналей прямоугольника
Каждая диагональ прямоугольника разделяет его на два равных прямоугольных треугольника. Длины диагоналей можно выразить через стороны прямоугольника, используя теорему Пифагора. Если стороны прямоугольника имеют длины a и b, то длина каждой диагонали равна квадратному корню из суммы квадратов сторон, то есть диагональ равна √(a^2 + b^2).
Например, если длина одной стороны прямоугольника равна 3, а длина другой стороны равна 4, то длина каждой диагонали будет равна √(3^2 + 4^2) = √(9 + 16) = √25 = 5. Таким образом, диагонали прямоугольника равны 5 единиц.
Равенство длин диагоналей прямоугольника является одним из его основных свойств. Это означает, что если две диагонали прямоугольника имеют одинаковую длину, то этот прямоугольник является квадратом. В противном случае, если диагонали имеют разные длины, прямоугольник является прямоугольником, но не квадратом.
Итак, диагонали прямоугольника — это особые отрезки, которые соединяют его вершины и играют важную роль в его свойствах и связях. Равенство длин диагоналей является одним из основных свойств прямоугольника и определяет его форму. Таким образом, понимание определения диагоналей прямоугольника позволяет лучше понять его геометрические свойства и использовать их в различных задачах и заданиях.
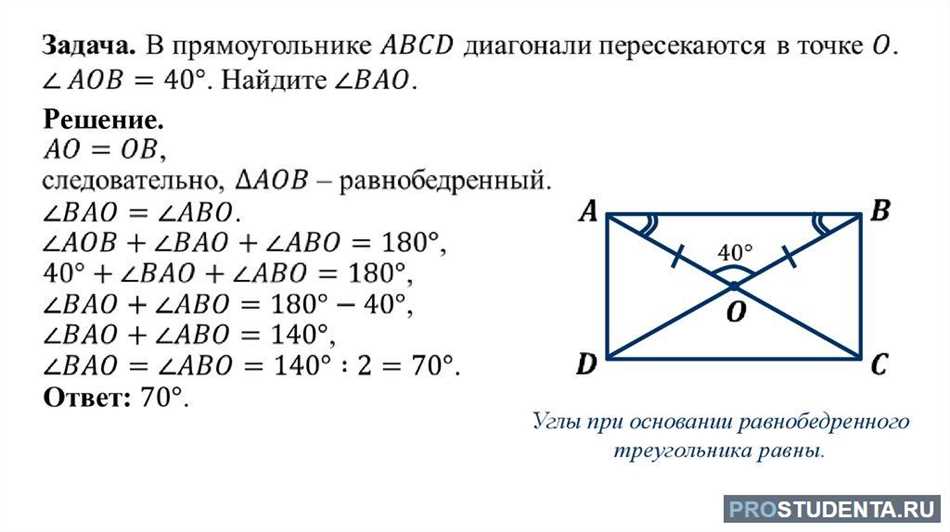
Взаимное положение диагоналей
Давайте рассмотрим диагонали прямоугольника. Диагональ — это линия, соединяющая две противоположные вершины. Если мы обозначим эти вершины как A, B, C и D, то диагонали будут AC и BD.
Взгляните на эти диагонали — они пересекаются в точке O, которая является центром прямоугольника. Возникает естественный вопрос: каково взаимное положение этих диагоналей?
Давайте проанализируем это. Для начала, давайте рассмотрим треугольник AOC. Он образован диагональю AC и двумя сторонами прямоугольника, AO и CO. Аналогично, треугольник BOD образован диагональю BD и двумя сторонами прямоугольника, BO и DO.
Мы знаем, что в прямоугольнике все углы прямые. Следовательно, угол AOC и угол BOD прямые углы. Это говорит о том, что треугольники AOC и BOD подобными.
Если два треугольника подобны, то их соответствующие стороны пропорциональны. Таким образом, соотношение длин сторон AO и BO, CO и DO будет одинаковое. А это означает, что AC и BD — равные диагонали.
Итак, мы доказали, что диагонали прямоугольника равны. Это удивительное свойство прямоугольника, которое можно понять и через геометрические соображения, и через математическое доказательство.
Постановка задачи
Задача состоит в доказательстве равенства диагоналей прямоугольника. Для этого нужно доказать, что диагонали прямоугольника АВ и CD равны между собой, то есть AB = CD.
Для начала, давайте вспомним основные свойства прямоугольника. Прямоугольник — это четырехугольник, у которого все углы прямые (равны 90 градусам).
Один из способов решить эту задачу — использовать свойства и определения прямоугольника. Если мы знаем, что углы прямые, то можно применить теорему Пифагора.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Вернемся к прямоугольнику. Если мы проведем диагонали AB и CD, то получим два прямоугольных треугольника. Они имеют общую гипотенузу, которая равна длине диагонали прямоугольника.
Теперь, чтобы доказать равенство диагоналей, мы можем применить теорему Пифагора к этим треугольникам. Если гипотеза о равенстве диагоналей верна, то сумма квадратов длин катетов в обоих треугольниках должна быть равна.
Давайте представим прямоугольник с длинами сторон a и b. Тогда диагональ прямоугольника AC будет гипотенузой треугольника ABC, а диагональ BD будет гипотенузой треугольника ABD.
В треугольнике ABC катеты равны a и b, поэтому согласно теореме Пифагора, квадрат длины гипотенузы AC будет равен a^2 + b^2.
Аналогично, в треугольнике ABD катеты также равны a и b, и квадрат длины гипотенузы BD будет равен a^2 + b^2.
Осталось только объединить две теоремы Пифагора, чтобы доказать, что сумма квадратов длин катетов в обоих треугольниках равна, и следовательно, диагонали равны между собой.
Доказательство равенства диагоналей прямоугольника
Для начала рассмотрим прямоугольник ABCD, где AB и CD — стороны прямоугольника, а AC и BD — его диагонали. Наша задача доказать, что AC = BD.
Воспользуемся теоремой Пифагора и расстоянием между точками в пространстве. Рассмотрим прямоугольный треугольник ACD. По теореме Пифагора:
AC2 = AD2 + CD2
Аналогично, рассмотрим прямоугольный треугольник ABD:
BD2 = AD2 + AB2
Так как AB = CD (так как прямоугольник ABCD является прямоугольником), у нас получается:
BD2 = AD2 + CD2
Сравнивая полученные выражения, можно увидеть, что AC2 = BD2. Так как расстояние никогда не может быть отрицательным, возможным решением является AC = BD.
Таким образом, доказано, что диагонали прямоугольника равны друг другу. Это свойство может быть полезно при решении различных геометрических задач и может быть использовано в соответствующих вычислениях.






