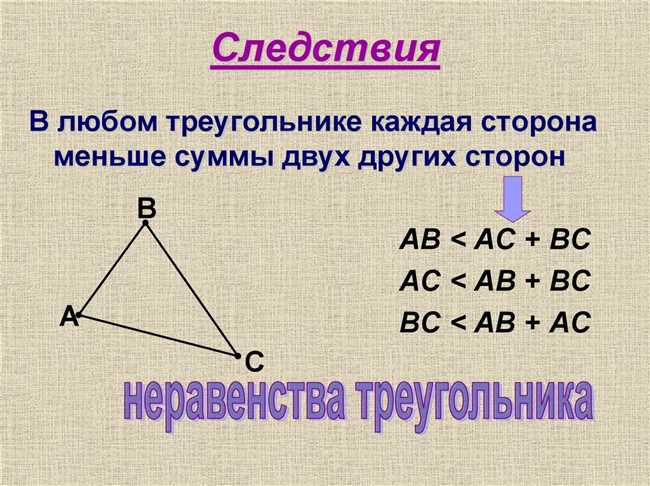
Неравенство треугольников — это основное правило геометрии, которое гласит, что сумма длин двух сторон треугольника всегда больше длины третьей стороны. Это правило может быть доказано и объяснено несколькими способами. Одним из способов является использование неравенства треугольников в контексте геометрической формулы, которая связывает стороны и углы треугольника. Другим способом является применение неравенства треугольников в контексте правила существования треугольника, которое утверждает, что для существования треугольника необходимо, чтобы сумма длин двух сторон была больше длины третьей стороны. Эти доказательства и объяснения помогают лучше понять и применять неравенство треугольников в геометрии.
Доказательство и объяснение неравенства треугольников
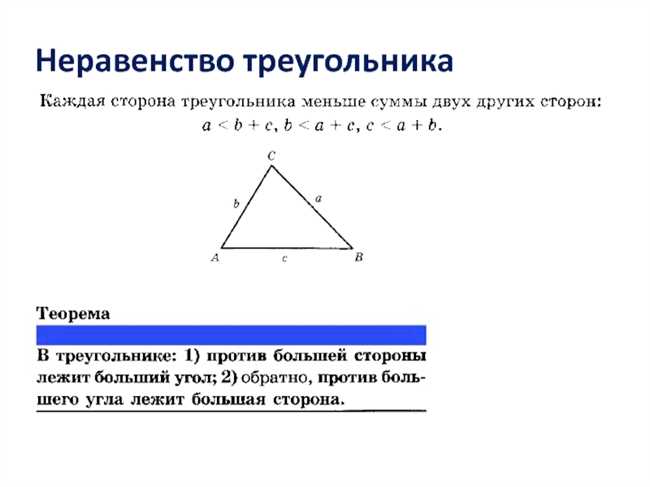
Первым шагом к пониманию неравенства треугольников является понятие о сумме углов треугольника. Все треугольники имеют сумму своих углов, равную 180 градусов. Это следует из основных принципов геометрии и треугольников.
Теперь мы можем перейти к доказательству существования неравенства треугольников. Допустим, у нас есть треугольник со сторонами a, b и c. Мы хотим доказать, что сумма двух сторон треугольника всегда больше третьей стороны.
Предположим, что третья сторона треугольника c больше суммы двух других сторон a и b. То есть, c > a + b. Теперь мы можем использовать это предположение и определение угла внутреннего треугольника, чтобы получить противоречие.
Давайте представим, что мы складываем две меньшие стороны треугольника (a и b), чтобы создать прямую линию. Теперь, если третья сторона c больше суммы a и b, то мы можем разместить эту сторону нашего треугольника так, что она будет лежать рядом с прямой линией, продлевая ее.
Теперь у нас есть треугольник с двумя меньшими углами и одним большим углом, который равен 180 градусов — по свойствам треугольника. Но этот большой угол не может быть равен 180 градусам, потому что сумма углов треугольника равна 180 градусам. Таким образом, мы получаем противоречие.
Из этого противоречия следует, что наше предположение не может быть верным и неравенство треугольников доказано. Сумма двух сторон всегда больше третьей стороны в треугольнике.
Почему это так важно? Неравенство треугольников имеет много применений в математике и реальном мире. Например, оно используется в сферах, связанных с построением, строительством и архитектурой. Также неравенство треугольников полезно при вычислении площади и показателей подобия треугольников.
- Неравенство треугольников помогает нам определить, может ли треугольник быть построен с заданными сторонами.
- Оно также помогает определить типы треугольников, такие как равносторонний, равнобедренный или обычный.
- Кроме того, неравенство треугольников может быть использовано для вычисления площади треугольника по формуле Герона.
Таким образом, неравенство треугольников является важным и полезным свойством, которое позволяет нам лучше понимать и использовать треугольники в различных ситуациях. Благодаря его доказательству и объяснению, мы можем применять эту теорию на практике и достигать лучших результатов в геометрии и других областях, где треугольники играют важную роль.
Определение неравенства треугольников
Это правило является основой для доказательства множества фактов и теорем о треугольниках, и позволяет сказать, что все треугольники, которые можно построить на плоскости, являются неравенствами треугольников.
Представь себе, что ты хочешь построить треугольник. У тебя есть три отрезка разной длины, и ты должен выбрать, какую сторону использовать как базовую. Неравенство треугольников говорит о том, что если ты выберешь две меньшие стороны, то их сумма всегда будет меньше третьей стороны.
Неравенство треугольников помогает нам понять, какие треугольники возможны и какие невозможны. Например, если у нас есть отрезок длиной 7 и отрезок длиной 3, то максимальная длина третьей стороны может быть 10 (сумма двух меньших сторон), а минимальная — 4 (разность двух сторон).
Это правило также позволяет нам решать задачи, связанные с треугольниками. Например, если известны длины двух сторон треугольника и нужно найти длину третьей стороны, мы можем использовать неравенство треугольников для определения диапазона возможных значений исходного треугольника.
Вот небольшой пример. Допустим, у нас есть треугольник со сторонами 5, 7 и x. Из неравенства треугольников мы знаем, что 5 + 7 > x. Зная это, мы можем определить, что x должно быть меньше суммы 5 и 7, то есть x < 12. Таким образом, мы устанавливаем ограничение для возможных значений x.
Таким образом, неравенство треугольников является фундаментальным понятием геометрии, которое помогает определить, какие треугольники могут существовать и решать задачи, связанные с длиной сторон треугольника.
Геометрическое доказательство неравенства треугольников
Представим, что у нас есть треугольник ABC, где AB соответствует первой стороне, BC — второй стороне, а AC — третьей стороне. Давайте изобразим этот треугольник на плоскости.
| AB | BC | AC |
 |
 |
 |
Теперь рассмотрим отрезок AB. Возьмем точку D на этом отрезке так, чтобы AD был равен третьей стороне AC. То есть AD = AC.
Изобразим отрезок AD и сторону BC.
| AD | BC |
 |
 |
Так как AD равен AC, то треугольник ACD является равносторонним треугольником. Следовательно, угол ACD равен 60 градусов.
Теперь рассмотрим треугольник ABD. У нас есть два равных отрезка — AD и AC. Из этого следует, что угол ADB равен углу ADC, то есть также 60 градусов.
| ADB | ADC |
 |
 |
Однако, сумма углов треугольника всегда равна 180 градусов. Значит, угол ABC равен 180 — 60 — 60 = 60 градусов.
Таким образом, мы доказали, что в остроугольном треугольнике с углом ABC равным 60 градусов, длина третьей стороны AC будет меньше суммы длин двух других сторон AB и BC. Это подтверждает неравенство треугольников.
Неравенство треугольников является важным инструментом в геометрии и широко применяется в различных задачах и теоремах. Оно помогает нам понять, какие треугольники могут существовать и какие существовать не могут. Надеюсь, что это доказательство помогло вам лучше понять этот принцип и его применение.
Алгебраическое доказательство неравенства треугольников
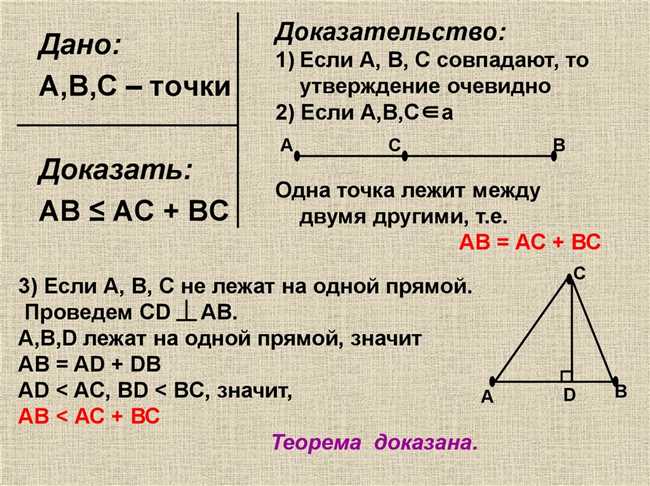
Но что если я скажу вам, что можно доказать неравенство треугольников с использованием алгебры? Да, вы все правильно поняли! Неравенство треугольников можно доказать с помощью алгебраических вычислений.
Представьте, что у нас есть треугольник ABC, где AB, BC и AC — это стороны треугольника, а a, b и c — их длины соответственно. Согласно неравенству треугольников, мы знаем, что сумма длин любых двух сторон всегда должна быть больше длины третьей стороны:
AB + BC > AC
BC + AC > AB
AC + AB > BC
Теперь давайте внедрим алгебру. Мы можем представить длины сторон треугольника в виде переменных: AB = a, BC = b и AC = c. Заменим переменные в неравенствах:
a + b > c
b + c > a
a + c > b
Теперь взглянем на эти неравенства под другим углом. Мы знаем, что сумма двух чисел всегда больше каждого из этих чисел по отдельности. Таким образом, мы можем написать:
a + b > a
a + b > b
b + c > b
b + c > c
a + c > a
a + c > c
На этом этапе мы можем использовать основной принцип алгебры: если два числа больше третьего числа, то их сумма также будет больше этого третьего числа. Поэтому доступна различные комбинации неравенств:
- a + b > c и b + c > a означает, что a + b + b + c > c + a;
- a + b > c и a + c > b означает, что a + b + a + c > b + c;
- b + c > a и a + c > b означает, что a + c + b + c > a + b;
Исходя из этих комбинаций, мы можем сказать, что a + b + c > a + b + c. Но это очевидно ведь сумма трех чисел всегда будет больше суммы тех же трех чисел. Из этого следует, что неравенство треугольников верно и алгебраически доказывается.
Теперь, когда мы понимаем, что неравенство треугольников можно доказать с использованием алгебры, мы можем лучше понять геометрические принципы и применения этого утверждения в реальной жизни. Теперь у вас есть способ взглянуть на неравенство треугольников с другой стороны и почувствовать уверенность в его истинности.
Интуитивное объяснение неравенства треугольников
Во-первых, давайте представим себе, что у нас есть треугольник, где одна из сторон намного короче, чем две другие. Теперь представьте, что вы пытаетесь закрыть этот треугольник, сложив его стороны друг на друга. Можете ли вы закрыть треугольник таким образом, что его короткая сторона лежит на верху, а две более длинные стороны лежат под ней? Нет, конечно. Попробуйте сделать это на практике, используя линейку и бумагу. Вы увидите, что треугольник не получится собрать.
Почему это происходит? Представьте себе, что вы взяли две длинные стороны треугольника и протянули их в прямую линию. Теперь, чтобы закрыть треугольник, вам нужно подвинуть гипотетическую вершину так, чтобы она легла на основание треугольника. Однако, если вы уменьшите длину короткой стороны, вершина будет ближе к основанию, что делает ее расстояние до длинных сторон длиннее. Следовательно, для того чтобы закрыть треугольник, третья сторона должна быть достаточно длинной, чтобы соединить остальные две стороны. Это и есть основная идея неравенства треугольников.
Таким образом, интуитивное объяснение неравенства треугольников заключается в том, что третья сторона треугольника должна быть достаточно длинной, чтобы соединить остальные две стороны и закрыть треугольник.
Применение неравенства треугольников в геометрии
Применение неравенства треугольников широко распространено, так как оно позволяет определить, существует ли треугольник с заданными сторонами. Например, если сумма длин двух сторон треугольника меньше или равна длине третьей стороны, то такой треугольник не может существовать. Это свойство можно использовать для проверки правильности построения треугольников.
Другим важным применением неравенства треугольников является определение типов треугольников. Например, если сумма длин двух сторон треугольника равна длине третьей стороны, то такой треугольник называется вырожденным или дегенеративным. Если сумма длин двух сторон меньше длины третьей стороны, то треугольник называется остроугольным. Если сумма длин двух сторон больше длины третьей стороны, то треугольник называется тупоугольным.






