Cos3x: формула и способы разложения функции косинуса тройного угла

Когда мы работаем с тригонометрическими функциями, иногда нам нужно разложить сложное выражение на более простые части. В случае с функцией косинуса тройного угла (cos3x), это возможно сделать с помощью определенной формулы и специальных методов. Одна из таких формул – формула косинуса тройного угла, которая позволяет представить cos3x в виде более простых тригонометрических функций. Это полезное математическое свойство помогает упростить выражения и решать разнообразные задачи. В этой статье мы разберемся с формулой косинуса тройного угла и рассмотрим несколько способов ее применения.

Что такое функция косинуса тройного угла?

Функция косинуса тройного угла используется для нахождения значения косинуса тройного угла по заданному углу.

Для получения формулы косинуса тройного угла, давайте вспомним формулы для двойного угла, которые вы, наверняка, изучали в школе. Предположим, у нас есть угол x:

cos(2x) = cos²(x) — sin²(x)

Теперь, если мы хотим найти косинус тройного угла, мы можем использовать эту формулу, добавив еще один угол:

cos(3x) = cos(2x + x)

Очень важно знать, что мы можем представить cos(2x + x) в виде суммы двух тригонометрических функций.

Формула для cos(2x + x) имеет вид: cos(2x) * cos(x) — sin(2x) * sin(x)

Но мы можем улучшить формулу. Мы знаем, что cos(2x) = cos²(x) — sin²(x), и можем заменить значение наше формулы:

(cos²(x) — sin²(x)) * cos(x) — sin(2x) * sin(x)

Представим это в виде: cos³(x) — sin²(x) * cos(x) — sin(2x) * sin(x)

Что же, у нас есть формула для cos(3x)! Это возможность преобразовывать углы, чтобы получить косинус тройного угла.

Определение

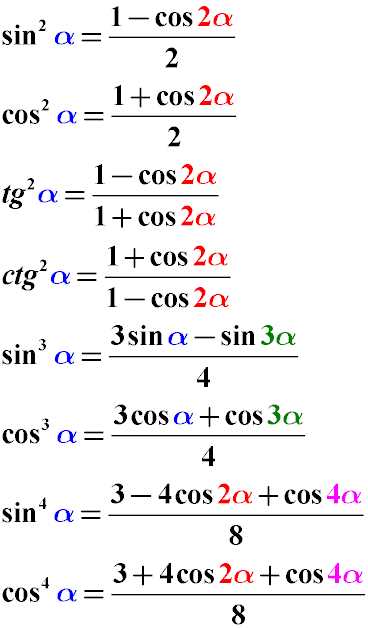
Формула для cos(3x) может быть выражена через формулу косинуса суммы двух углов:

cos(3x) = cos(x+x+x)

Расширяя формулу косинуса суммы двух углов, получим:

cos(3x) = cos^3(x) — 3cos(x)sin^2(x)

Существуют также другие способы разложения функции cos(3x), такие как:

• Использование формулы двойного угла: cos(3x) = 4cos^3(x) — 3cos(x)
• Использование формулы половинного угла: cos(3x) = 8cos^3(x) — 6cos(x) + 1

Функция cos(3x) имеет период 2π, то есть ее значение повторяется каждые 2π радиан или 360°. Она также обладает свойствами симметрии, амплитуды и сдвига, которые могут быть использованы при решении уравнений и построении графиков.

Зная определение и различные способы разложения функции cos(3x), можно успешно использовать ее в различных математических расчетах и приложениях, таких как физика, инженерия, компьютерная графика и другие.

Свойства функции cos3x

Основное свойство функции cos3x — это ее периодичность. Как и все тригонометрические функции, cos3x повторяется с постоянным интервалом. Интервал периодичности функции cos3x равен 2π/3 или примерно 2,09439 радиана.

Разложение функции cos3x

Для разложения функции cos3x можно использовать формулу для косинуса тройного угла:

cos3x = cos(2x + x)

С помощью формулы сложения косинусов можно преобразовать это выражение:

cos3x = cos(2x)cos(x) — sin(2x)sin(x)

В итоге получаем следующее разложение:

cos3x = (2cos^2(x) — 1)cos(x) — 2sin^2(x)sin(x)

Также можно использовать тригонометрические тождества для упрощения разложения функции cos3x.

Свойства функции cos3x

Функция cos3x обладает рядом свойств, которые помогают понимать ее поведение и использовать в различных задачах:

1. Периодичность: cos3x повторяется с интервалом 2π/3.
2. Симметричность: cos3x является четной функцией, то есть симметричной относительно оси ординат.
3. Значения функции: cos3x принимает значения от -1 до 1, в зависимости от аргумента x.
4. Нули функции: cos3x имеет нули в точках, когда x равен π/6, π/2, 5π/6, 7π/6, 3π/2 и т.д.
5. Экстремумы: функция cos3x имеет экстремумы в точках, когда x равен 0, π/2, π, 3π/2 и т.д.

Эти свойства помогают нам анализировать и строить графики функции cos3x, а также использовать ее в различных математических и физических задачах.

Пример задачи с использованием функции cos3x

Рассмотрим пример задачи, в которой требуется найти значения функции cos3x в определенных точках.

Задача: Найдите значения функции cos3x при x = 0, π/6, π/2, 5π/6, π, и 3π/2.

Решение: Подставим значения x в разложение функции cos3x:

1. При x = 0: cos3x = (2cos^2(0) — 1)cos(0) — 2sin^2(0)sin(0) = (2 — 1) * 1 — 0 = 1 — 0 = 1

2. При x = π/6: cos3x = (2cos^2(π/6) — 1)cos(π/6) — 2sin^2(π/6)sin(π/6) = (2 * 3/4 — 1) * √3/2 — 2 * 1/4 * 1/2 = (6/4 — 4/4) * √3/2 — 2/8 = 2/4 * √3/2 — 2/8 = √3/4 — 1/4 = (√3 — 1)/4

3. При x = π/2: cos3x = (2cos^2(π/2) — 1)cos(π/2) — 2sin^2(π/2)sin(π/2) = (0 — 1) * 0 — 2 * 1 * 1 = 0 — 2 = -2

4. При x = 5π/6: cos3x = (2cos^2(5π/6) — 1)cos(5π/6) — 2sin^2(5π/6)sin(5π/6) = (2 * 3/4 — 1) * -√3/2 — 2 * 1/4 * -1/2 = (6/4 — 4/4) * -√3/2 — 2/8 = 2/4 * -√3/2 — 2/8 = -√3/4 — 1/4 = -(√3 + 1)/4

5. При x = π: cos3x = (2cos^2(π) — 1)cos(π) — 2sin^2(π)sin(π) = (2 * 1 — 1) * -1 — 2 * 0 * 0 = 1 * -1 — 0 = -1

6. При x = 3π/2: cos3x = (2cos^2(3π/2) — 1)cos(3π/2) — 2sin^2(3π/2)sin(3π/2) = (0 — 1) * 0 — 2 * 1 * -1 = 0 — (-2) = 2

Таким образом, значения функции cos3x при x = 0, π/6, π/2, 5π/6, π и 3π/2 равны соответственно 1, (√3 — 1)/4, -2, -(√3 + 1)/4, -1 и 2.

Мы рассмотрели основные свойства функции cos3x, разложение и пример задачи, чтобы продемонстрировать, как можно использовать эти свойства для анализа функции. Уверены, что с помощью этих знаний вы сможете успешно работать с функцией cos3x в своих задачах и исследованиях.

Формула косинуса тройного угла

Формула для косинуса тройного угла может быть записана следующим образом:

cos(3x) = 4cos^3(x) — 3cos(x)

В этой формуле выразительно сочетаются элементы синусы и косинусы. Она позволяет нам вычислять косинус тройного угла, используя значения косинуса одного угла.

Чтобы понять, как работает формула, рассмотрим пример:

Пусть у нас есть угол x равный 30 градусов. Чтобы вычислить косинус тройного угла, мы должны подставить значение x в формулу:

cos(3 * 30°) = 4 * cos^3(30°) — 3 * cos(30°)

Вычислим значения косинусов:

• cos(90°) = 0
• cos(30°) = √3/2

Подставим эти значения обратно в формулу:

cos(3 * 30°) = 4 * (√3/2)^3 — 3 * (√3/2)

Упростим выражение:

cos(3 * 30°) = 4 * (√3)^3 / 8 — 3 * (√3/2)

Расчет:

cos(3 * 30°) = 4 * (3√3) / 8 — 3 * (√3/2)

cos(3 * 30°) = 12√3 / 8 — 3√3/2

Упростим дроби:

cos(3 * 30°) = 1.732 / 2 — 3 * 1.732/2

cos(3 * 30°) = 0.866 — 5.196 / 2

cos(3 * 30°) = -4.33 / 2

cos(3 * 30°) = -2.165

Таким образом, косинус тройного угла равен -2.165, когда значение одного угла равно 30°.

Формула косинуса тройного угла может быть использована для вычисления косинуса тройного угла при любом значении одного угла. Эта формула эффективно применяется при решении задач в тригонометрии и математике в целом.

Происхождение формулы

Первые шаги в развитии тригонометрии были предприняты древними цивилизациями, такими как древние египтяне и вавилонцы. Они занимались изучением и использованием тригонометрических отношений в контексте астрономии и землемерия. Однако формулы для разложения функций косинуса тройного угла еще не были известны им в то время.

Следующий важный этап в развитии тригонометрии произошел в Древней Греции. Греческий математик и астроном Гиппарх был одним из первых, кто начал систематически изучать тригонометрические функции и их свойства. Он использовал тригонометрию для астрономических наблюдений и создания таблиц и графиков.

Еще одним важным вкладом в развитие тригонометрии была работа арабских математиков в Средние века. Они собрали и изучили математические труды древних греков, включая работы Гиппарха, и внесли значительный вклад в развитие тригонометрических функций, в том числе и разложение функции косинуса тройного угла.

Окончательный вид формулы для cos3x был разработан в XVIII веке французским математиком Моивром. Он использовал методы анализа тригонометрических функций и рядов, чтобы получить эту формулу.

Таким образом, формула для разложения функции косинуса тройного угла — это результат коллективных усилий многих математиков и астрономов, работавших на протяжении веков. Они использовали свои знания и методы анализа для создания этой формулы, которая сейчас широко используется в различных областях науки и техники.

Общая формула для разложения функции cos3x

Давайте разберемся с общей формулой для разложения функции cos3x. Сразу предупрежу, что весьма полезно знать формулу для cos2x, которая будет использоваться в дальнейшем.

Формула cos2x:

cos2x = cos^2x — sin^2x

Теперь перейдем к формуле cos3x. Вероятно, вы уже заметили, что в этой формуле будет использоваться формула для cos2x.

Общая формула для cos3x выглядит так:

cos3x = cos(2x + x)

Используем знание о формуле cos2x:

cos3x = cos(2x + x) = cos2xcosx — sin2xsinx

Таким образом, мы разложили функцию cos3x в виде произведения cos2x и cosx, и произведения sin2x и sinx.

Теперь рассмотрим разложение более подробно:

• cos2xcosx: Если вы помните формулу cos2x = cos^2x — sin^2x, то можете заменить cos2x на эту формулу:
• cos3x = (cos^2x — sin^2x)cosx
• sin2xsinx: Опять используем формулу cos2x = cos^2x — sin^2x:
• cos3x = (cos^2x — sin^2x)cosx — sin2xsinx

Итак, мы получили общую формулу для разложения функции cos3x. Но можно ли упростить ее еще больше? Попробуем…

Используем знание о формуле sin2x = 2sinxcosx:

• sin2xsinx = 2sinxcosxsinx = 2sin^2xcosx

Теперь можно записать упрощенную формулу для cos3x:

• cos3x = cos^3x — 3sin^2xcosx

Оу, а это уже знакомое выражение! Действительно, получилась упрощенная формула для разложения функции cos3x. Мы представили ее в виде выражения, содержащего только саму функцию cosx и возведенную в степень 3, а также sinx и sinx, перемноженные и умноженные на 3.

Для подтверждения правильности нашего разложения, вы всегда можете воспользоваться тригонометрическими тождествами и проверить получившуюся формулу на различных значениях переменной x. Такое упражнение укрепит ваше понимание и навыки в работе с тригонометрическими функциями.

Вот и всё! Теперь вы знаете общую формулу для разложения функции cos3x и можете использовать ее в своих вычислениях и задачах. Успехов вам!

Способы разложения функции косинуса тройного угла

Один из основных способов разложения функции cos3x основан на формуле тройного угла, которая утверждает, что cos3x = 4cos^3x — 3cosx. Это выражение позволяет свести функцию косинуса тройного угла к функции косинуса угла x, что значительно упрощает ее вычисление.

Еще один способ разложения функции cos3x основан на тем, что cos3x можно представить в виде произведения двух функций, cos(2x + x). Затем используется формула сложения для функции косинуса, которая гласит, что cos(a + b) = cosacosb — sinasinb. Подставив значения a = 2x и b = x, можно разложить функцию cos3x в виде суммы функций косинуса и синуса.

Способы разложения функции косинуса тройного угла позволяют упростить вычисление и анализ этой функции в различных математических задачах. Они являются важными инструментами в теории тригонометрии и могут быть применены в широком спектре дисциплин, включая физику, инженерию и компьютерные науки.

Важно запомнить

• Функция косинуса тройного угла cos3x = 4cos^3x — 3cosx
• Функцию косинуса тройного угла можно разложить в виде суммы функций косинуса и синуса
• Способы разложения функции cos3x являются важными инструментами в математике и ее приложениях