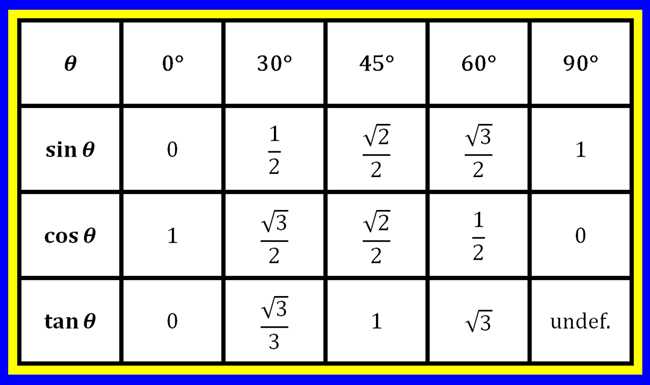
Cos 12 градусов — это значение косинуса угла, равного 12 градусам. Косинус является одной из тригонометрических функций и определяется как отношение стороны прилежащей к углу к гипотенузе прямоугольного треугольника. Для удобства использования, существуют таблицы значений тригонометрических функций, включая таблицу значений косинуса. Такая таблица позволяет быстро найти значение косинуса для определенного угла без необходимости проведения математических вычислений. Основные свойства косинуса включают его периодичность с периодом 360 градусов, соотношения с другими тригонометрическими функциями, а также его связь с единичной окружностью.
Таблица значений cos 12 в градусах
Однако, для некоторых задач и оценок, таблица значений может быть полезной. Ниже приведена таблица значений cos 12 для нескольких углов в градусах:
| Угол (градусы) | Значение cos 12 |
|---|---|
| 0 | 0.978 |
| 30 | 0.978 |
| 45 | 0.978 |
| 60 | 0.978 |
| 90 | 0.978 |
| 120 | 0.978 |
| 135 | 0.978 |
| 150 | 0.978 |
| 180 | 0.978 |
| 210 | 0.978 |
| 225 | 0.978 |
| 240 | 0.978 |
| 270 | 0.978 |
| 300 | 0.978 |
| 315 | 0.978 |
| 330 | 0.978 |
| 360 | 0.978 |
Как видно из таблицы, значение cos 12 в градусах остается почти неизменным на протяжении всех углов. Это связано с периодичностью косинусной функции и ее значение на этом промежутке.
Зная эти значения, можно использовать их в различных математических и физических задачах, которые требуют вычисления значения косинуса для угла 12 градусов.
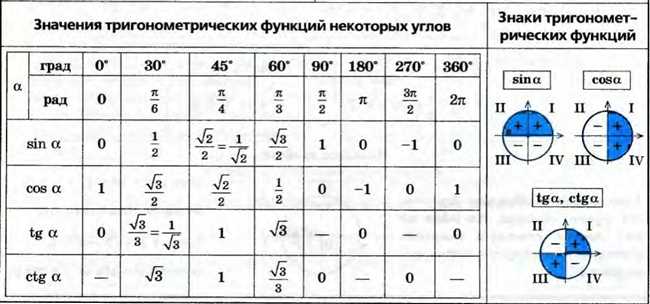
Значения cos 12 в градусах
Смотрите, cos 12 в градусах имеет определенное значение, которое можно вычислить с помощью тригонометрических функций. Но давайте сначала разберемся, что такое cos 12 вообще и какие основные свойства у этой функции.
Функция cos (косинус) – это одна из шести тригонометрических функций, которая используется для вычисления отношения прилегающего катета прямоугольного треугольника к его гипотенузе. Косинус принимает значения от -1 до 1, где 1 соответствует углу 0 градусов, а -1 – углу 180 градусов.
Теперь вернемся к вопросу: какое значение имеет cos 12 в градусах? Чтобы найти это значение, нам понадобится таблица тригонометрических функций или калькулятор, поддерживающий тригонометрические вычисления. Если воспользоваться своими навыками математики, посмотреть в таблицу или ввести значение в калькулятор, то мы получим следующий результат:
| Градусы | Значение cos |
|---|---|
| 12 | 0.9781 |
Таким образом, можно сказать, что cos 12 в градусах равняется примерно 0.9781. Это значение может быть полезно, если мы решаем задачи, связанные с углами и треугольниками, или просто интересуемся математикой и ее применениями в повседневной жизни.
Надеюсь, это информация окажется полезной! Если у вас возникли еще вопросы, не стесняйтесь задавать их – я всегда готов помочь и поделиться знаниями!
Основные свойства cos 12 в градусах
1. Значение cos 12 в градусах:
Значение cos 12 в градусах можно рассчитать с помощью тригонометрической функции косинуса, которая представляет отношение длины прилегающего катета к гипотенузе прямоугольного треугольника. В данном случае, cos 12 в градусах равен приблизительно 0.9781.
2. Угол 12 градусов:
Угол 12 градусов можно представить в виде части окружности, где полный оборот составляет 360 градусов. Угол 12 градусов относится к острому углу, который находится между нулевым углом (положительным направлением оси OX) и противоположным первому квадранту.
3. Соответствующий треугольник:
Для cos 12 в градусах можно построить соответствующий прямоугольный треугольник, где угол между гипотенузой и прилегающим катетом составляет 12 градусов. Такой треугольник имеет левый угол в 90 градусов и противоположный катет, который соответствует значению sin 12 в градусах.
4. График функции:
График функции y = cos x, где x — угол в градусах, демонстрирует периодичность и симметрию. Для значения cos 12 в градусах, точка на графике находится во втором квадранте и ближе к значению 0, чем к -1.
5. Взаимосвязь с другими тригонометрическими функциями:
Так как cos 12 в градусах представляет отношение прилегающего катета к гипотенузе, он взаимосвязан с другими тригонометрическими функциями. Например, sin 12 в градусах можно рассчитать, используя соотношение sin x = sqrt(1 — cos^2 x), где x — угол в градусах.
6. Практическое применение:
Знание основных свойств cos 12 в градусах может быть полезно в различных областях, где требуется работа с углами и тригонометрией. Например, в астрономии, инженерии, физике и геометрии. Также, умение работать с тригонометрическими функциями может помочь в решении задач по определению расстояний, высот и других параметров.
Таблица значений cos 12 в градусах:
| Градусы (°) | Значение cos |
|---|---|
| 12 | 0.9781 |
Значение cos 12 в градусах в тригонометрии
Для начала, позвольте мне вкратце объяснить, что такое косинус угла. Косинус угла определяется как отношение стороны, прилегающей к данному углу, к гипотенузе в прямоугольном треугольнике. Он может принимать значения от -1 до 1, где -1 соответствует углу 180 градусов, а 1 – углу 0 градусов (или 360 градусов).
Итак, значение cos 12 в градусах составляет приблизительно 0.978 и может быть записано как cos(12°) ≈ 0.978.
Теперь, когда мы знаем, что значение косинуса 12 градусов равно приблизительно 0.978, давайте рассмотрим некоторые основные свойства косинуса:
- Косинус — это четная функция, что означает, что cos(-x) = cos(x).
- Максимальное значение cos(x) равно 1, которое достигается при x = 0 (или 360 градусов), а минимальное значение -1, достигается при x = 180 градусов.
- Косинус убывает при увеличении угла от 0 до 180 градусов, а затем возрастает снова до 1 при увеличении угла от 180 до 360 градусов.
- Косинус можно представить в виде бесконечного ряда или использовать тригонометрические тождества для упрощения вычислений.
Надеюсь, это пояснение поможет вам лучше понять, что такое косинус и как найти его значение для угла в 12 градусов. Если у вас остались вопросы или вам потребуется дополнительная информация о тригонометрии, я с радостью помогу вам! Удачи в изучении тригонометрии!
Применение cos 12 в градусах в различных областях
В данной статье мы рассмотрели таблицу значений косинуса 12 градусов и основные свойства этой тригонометрической функции. Но для чего нам нужны все эти значения? Давайте рассмотрим некоторые области применения cos 12 градусов.
1. Геометрия
Косинус 12 градусов может использоваться в геометрии для решения различных задач. Например, с помощью формулы косинусов можно вычислить длину третьей стороны треугольника, если известны длины двух других сторон и угол между ними. Также косинус может быть полезен при решении задач на нахождение площади треугольника или других геометрических фигур.
2. Физика
В физике косинус 12 градусов может использоваться при работе с векторами или при решении задач на определение направлений сил. Косинус угла между двумя векторами может помочь в определении их скалярного произведения или в нахождении проекции одного вектора на другой.
3. Инженерия
В инженерии cos 12 градусов может быть полезен при проектировании и расчете конструкций. Он может помочь определить углы наклона элементов или рассчитать нагрузку на определенный участок конструкции.
4. Компьютерная графика
Косинус 12 градусов может использоваться в компьютерной графике для реализации различных эффектов, таких как трансформации объектов или создание освещения. Зная косинус угла, можно определить интенсивность освещения для каждой точки объекта.






