Что такое середина отрезка в геометрии для 7 класса?

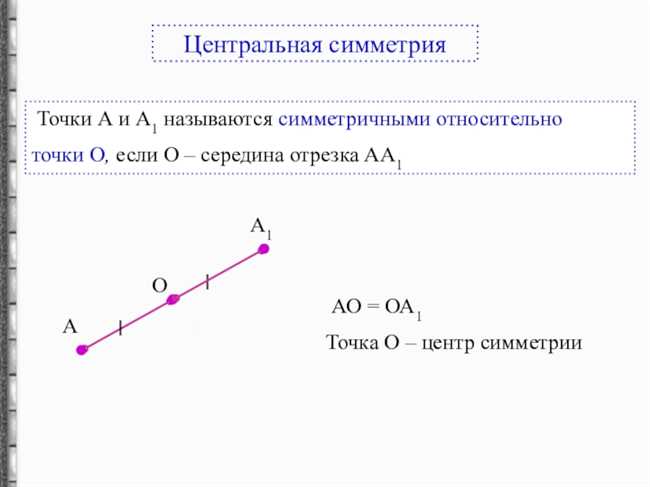
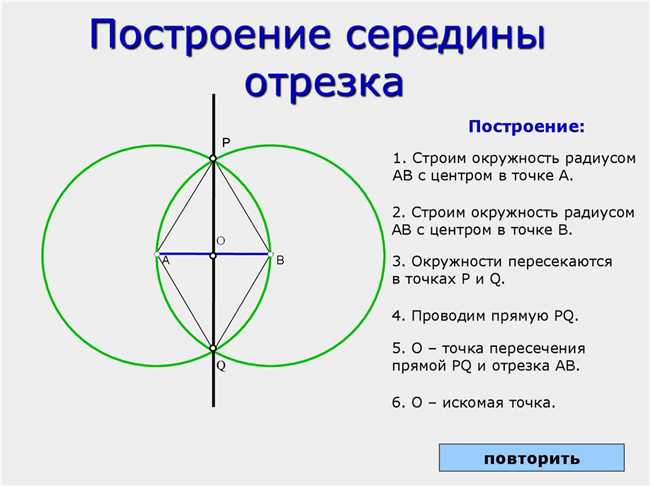
В геометрии 7 класса середина отрезка — это точка, которая делит отрезок на две равные части. Она находится на равном удалении от концов отрезка и является его симметричным центром. Середина отрезка обозначается прописными буквами, например, точка М. Для нахождения середины отрезка можно использовать различные методы: построение окружности радиусом, равным половине длины отрезка, пересечение отрезка с прямой, проведенной через его концы, или арифметическую формулу для нахождения среднего значения координат концов отрезка. Знание понятия середины отрезка важно для решения задач по геометрии, в том числе для построения фигур и нахождения их геометрических параметров.

Определение середины отрезка

Для нахождения середины отрезка можно использовать различные методы. Один из них — построение перпендикуляра, проходящего через середину отрезка. Для этого можно использовать циркуль и линейку, или же воспользоваться готовыми инструментами на компьютере.

Также середина отрезка может быть найдена аналитически, используя координаты начала и конца отрезка. Формула для нахождения координат середины отрезка выглядит следующим образом:

Середина отрезка имеет координаты:

• x = (x₁ + x₂) / 2
• y = (y₁ + y₂) / 2

Где (x₁, y₁) и (x₂, y₂) — координаты начала и конца отрезка соответственно.

Середина отрезка является важным понятием в геометрии, она позволяет решать различные задачи, связанные с расположением точек на отрезке. Например, зная координаты середины отрезка, можно найти расстояние между началом и концом этого отрезка. Также середина отрезка может быть использована для поиска пропорций или доказательства геометрических теорем.

Понимание того, что такое середина отрезка, поможет вам лучше понять геометрию и решать задачи, связанные с расположением точек и отрезков на плоскости. Удачи в изучении геометрии!

Как найти середину отрезка

Для того чтобы найти середину отрезка, необходимо выполнить следующие шаги:

1. Измерьте длину отрезка. Для этого используйте линейку или другой измерительный инструмент.
2. Разделите длину отрезка пополам.
3. Найдите точку, которая находится на половине отрезка. Эта точка будет серединой отрезка.

Давайте рассмотрим пример. Предположим, у нас есть отрезок длиной 10 см. Чтобы найти его середину, мы должны разделить его длину пополам. В данном случае, это будет 5 см.

Когда мы нашли середину, мы можем использовать эту информацию для решения различных задач. Например, если нам нужно разделить отрезок на равные части, мы можем измерить расстояние от середины до каждого конца отрезка и отметить эти точки.

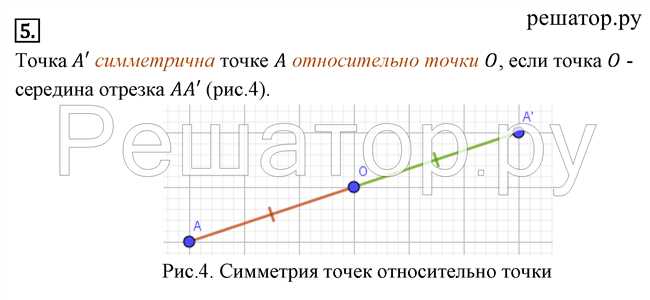
Также стоит отметить, что середина отрезка является центром симметрии. Это означает, что любая точка, отображенная симметрично относительно середины отрезка, будет также являться серединой отрезка.

Свойства середины отрезка

1. Равномерность

Первое свойство середины отрезка — она делит его на две равные части. Это значит, что расстояние от начала отрезка до середины равно расстоянию от середины до конца отрезка. Например, если отрезок имеет длину 10 единиц, то расстояние от начала до середины будет 5 единиц, а от середины до конца — также 5 единиц.

2. Симметричность

Второе свойство середины отрезка — она является симметричной относительно каждой точки на отрезке. Это означает, что если мы нарисуем отрезок и отметим точку середины, то линии, соединяющие середину с концами отрезка, будут одинаковой длины и будут располагаться симметрично относительно точки середины.

3. Примеры использования

Середина отрезка имеет много применений в геометрии и в реальной жизни. Она используется для нахождения среднего значения, для нахождения центра масс тел, для построения симметричных фигур и многого другого. К примеру, если мы знаем значения двух крайних точек на графике, то мы можем найти середину и использовать ее для предсказания значения промежуточной точки.

Таким образом, середина отрезка — это важная концепция в геометрии, которая имеет множество свойств и применений. Она позволяет нам лучше понять отношения и взаимодействия в геометрических объектах и может быть использована в различных ситуациях как в учебе, так и в повседневной жизни.

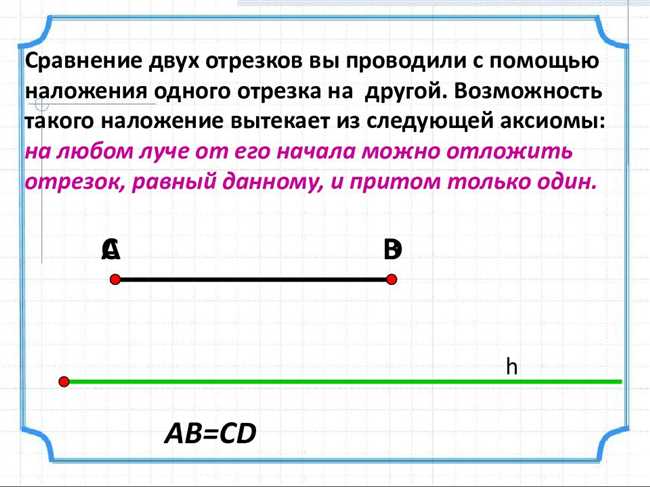
Равенство отрезков, имеющих общую середину

Чтобы отрезки АВ и CD были равны, они должны иметь общую середину. Середина отрезка – это точка, которая располагается на полпути между его концами. Если у отрезков АВ и CD есть одна и та же середина, то они будут равны друг другу.

Для того чтобы убедиться в равенстве отрезков, имеющих общую середину, можно провести следующие шаги:

1. Найди середину отрезка АВ. Для этого нужно взять его две концевые точки и найти точку, которая будет находиться ровно посередине между ними.
2. Проведи от середины линию, которая пересекает отрезок CD.
3. Если эта линия пересекает отрезок CD ровно в его середине, то отрезки АВ и CD равны.

Таким образом, когда отрезки имеют общую середину, мы можем быть уверены в их равенстве. Равные отрезки имеют одинаковую длину, поэтому они могут использоваться для измерений и построений в геометрии.

Но любые равные отрезки не обязательно должны иметь общую середину. Они могут быть расположены в разных местах на плоскости или даже быть параллельными.

Также стоит отметить, что равные отрезки можно сравнивать именно в контексте равенства их длин. Они могут иметь разные положения на плоскости и углы между собой, но их длина будет одинаковой.

Понимание равенства отрезков и их общей середины является важным концептом в геометрии. Оно помогает нам сравнивать и измерять отрезки, а также строить различные фигуры и конструкции с использованием равных отрезков.

Отрезок с разными серединами

Во-первых, давайте вспомним, что значит быть серединой отрезка. Когда отрезок делится на две равные части, точка, которая делит его на половину, является его серединой. Найдя середину отрезка, мы можем быть уверены, что расстояния от начальной и конечной точек до середины будут одинаковыми. Это свойство является основным для разделения отрезка на две половины.

Теперь предположим, что отрезок имеет различные середины. Это означает, что есть несколько точек, которые делят отрезок на равные части. Но как такое может быть, если середина — единственная точка, которая делит отрезок на половины?

Однако, давайте взглянем на это с другой стороны. Если мы предположим, что отрезок имеет различные середины, это означает, что у нас есть несколько точек, которые равноудалены от начальной и конечной точек отрезка. В таком случае, каждая из этих точек также может быть рассмотрена как середина отрезка.

Разные середины отрезка могут быть полезны в различных ситуациях. Например, при построении перпендикулярных линий, основываясь на разных серединах отрезка, можно получить разные результаты. Это позволяет нам создавать разнообразные геометрические фигуры и конструкции.

Таким образом, отрезок с различными серединами представляет собой ситуацию, когда есть несколько точек, которые равноудалены от начальной и конечной точек отрезка. В геометрии эта особенность может быть использована для создания разнообразных фигур и вариантов построений. Чтобы найти середину отрезка, необходимо просто найти точку, которая делит его на две равные части.

Заключение

Мы рассмотрели несколько примеров задач, в которых требуется находить середину отрезка, а также использовать свойства середины отрезка для решения геометрических задач. Задачи могут быть разнообразными, начиная от вычисления координат середины отрезка до определения положения других точек относительно данной середины.

Знание свойств и умение работать с серединой отрезка позволит нам решать задачи, связанные с геометрией, эффективно и точно. Отрезки и их середина являются базовыми понятиями в геометрии и являются основой для более сложных геометрических конструкций. Уверенное владение этими понятиями открывает перед нами широкие возможности в решении различных задач.