Касательная к окружности – это прямая, которая касается окружности в одной точке. Когда рисуется окружность на плоскости, можно провести бесконечно много прямых, которые пересекают окружность в двух точках. Но только одна прямая может коснуться окружности в одной точке и не пересекать ее. Эта прямая называется касательной. Теорема о свойстве касательной говорит о том, что касательная к окружности в заданной точке перпендикулярна радиусу, проведенному в этой точке. Эта теорема доказывается и используется в геометрии для решения различных задач, связанных с окружностями.
Тема: Какая прямая называется касательной к окружности?
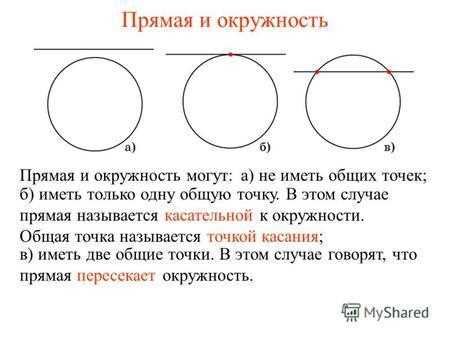
Помимо этого, касательная имеет важное геометрическое свойство: все точки касательной находятся по одну сторону окружности. Это означает, что если мы проведем прямую, которая пересечет окружность в двух точках, то она не может быть касательной. Таким образом, касательная — это прямая, которая идет только через одну точку на окружности и находится полностью внутри окружности.
А теперь представьте, что вы нарисовали касательную к окружности и провели радиус из точки касания до центра окружности. Угол между касательной и радиусом всегда будет прямым, это еще одна важная особенность касательной. Из этого следует, что касательная к окружности и радиус касаются друг друга под прямым углом.
Теперь, что вы знаете, как определить касательную к окружности, давайте докажем теорему о ее свойствах.
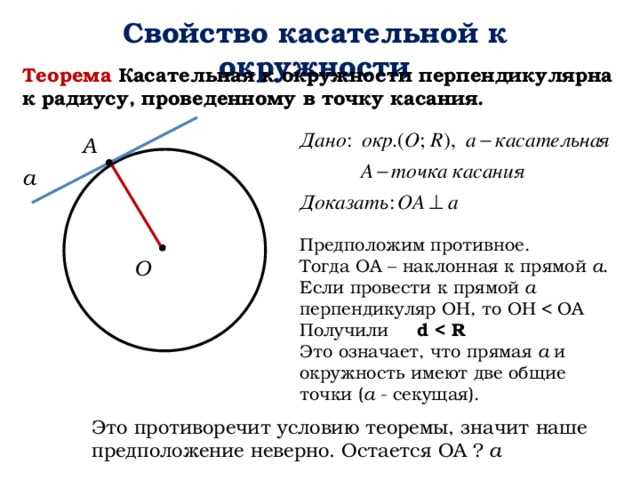
Теорема:

Касательная к окружности перпендикулярна радиусу, проведенному в точке касания.
Доказательство:
Предположим, что у нас есть окружность с центром O и радиусом R. Пусть A будет точкой, в которой касательная касается окружности, и пусть OA будет радиусом, проведенным в точке касания.
Посмотрим на треугольник OAB, где O — центр окружности, A — точка касания и B — другая точка на окружности.
Так как интуитивно мы знаем, что касательная к окружности перпендикулярна радиусу, мы предположим, что угол OAB — прямой. Наша задача — это доказать это предположение.
- Косинусы углов треугольника: В треугольнике OAB, так как угол OAB прямой, косинус этого угла равен нулю.
- Знание свойств окружности: Мы также знаем, что отрезок OA — это радиус окружности, поэтому |OA| = R.
Теперь рассмотрим угол OAB из косинуса извлекаем значения:
| O | A | B | |
|---|---|---|---|
| Координаты (x, y) | (0, 0) | (x, y) | (x’, y’) |
- OA^2 = x^2 + y^2
- AB^2 = (x’ — x)^2 + (y’ — y)^2
Теперь применим теорему Пифагора к треугольнику OAB, используя эти значения:
OA^2 + AB^2 = R^2 + (x’ — x)^2 + (y’ — y)^2
Распространяя это уравнение, мы получаем:
x^2 + y^2 + (x’ — x)^2 + (y’ — y)^2 = R^2 + (x’ — x)^2 + (y’ — y)^2
Упрощение этого уравнения дает:
x^2 + y^2 = R^2, что означает, что OA^2 = R^2, а значит, OA = R.
Таким образом, мы доказали, что угол OAB равен 90 градусам, что означает, что касательная к окружности перпендикулярна радиусу, проведенному в точке касания.
Итак, вот доказательство теоремы о свойстве касательной к окружности.
Раздел 2: Определение касательной к окружности
Чтобы лучше понять это определение, представьте, что вы берете карандаш и касаетесь им поверхности шарика. Изображено? Подобным образом касательная к окружности может быть представлена как прямая, которая лишь слегка прикасается к окружности в одной точке.
Если мы хотим доказать теорему о свойстве касательной к окружности, нужно учесть следующее:
- Касательная, проведенная к окружности, перпендикулярна радиусу, проведенному к точке касания
- Любой радиус, проведенный к точке касания, является перпендикуляром к касательной, проведенной в этой точке
Давайте рассмотрим пример для лучшего понимания. Представьте себе окружность и проведенный из ее центра радиус. Когда этот радиус касается окружности в какой-то точке, он становится касательной. Правильно?
Итак, теорема о свойстве касательной к окружности утверждает, что радиус, проведенный к точке касания, является перпендикуляром к касательной, проведенной в этой точке. То есть, если мы проведем радиус от центра окружности до точки касания, а затем проведем прямую, которая будет подчиняться определению касательной, эти две прямые будут перпендикулярны.
Надеюсь, теперь вы понимаете, что такое касательная к окружности и как это свойство может быть доказано. Касательная — это прямая, которая касается окружности в одной точке, не пересекая ее, и перпендикулярна радиусу, проведенному в этой точке касания.
Раздел 3: Свойства касательной к окружности
Теорема о свойстве касательной к окружности гласит:
Если прямая касается окружности в точке, то она перпендикулярна радиусу, проведенному в эту точку.
Это свойство касательной можно доказать, используя геометрическую конструкцию.
Рассмотрим окружность O с центром в точке A. Пусть B — произвольная точка на окружности, а T — точка касания прямой BT с окружностью O. Если провести радиус AO, то он будет перпендикулярен прямой BT.
Чтобы это доказать, рассмотрим треугольник OAT. У него одна сторона равна радиусу, другая сторона — радиус BT, а угол между этими сторонами — 90 градусов (равенство угла между касательной и радиусом). Из свойства прямоугольного треугольника следует, что сторона, противолежащая прямому углу, будет перпендикулярна к гипотенузе.
Таким образом, мы доказали, что прямая BT, касающаяся окружности O в точке T, является перпендикуляром для радиуса AO, проведенного в эту точку.
Это свойство касательной к окружности имеет широкое применение в геометрии и физике. Например, оно используется в построении оптических систем, в видеокамерах и других устройствах, где требуется точное изображение.
Раздел 4: Доказательство теоремы о свойстве касательной
В этом разделе будем рассматривать доказательство теоремы о свойстве касательной к окружности.
Теорема: Прямая, проведенная через точку касания окружности и перпендикулярная радиусу в этой точке, называется касательной к окружности.
Доказательство: Рассмотрим окружность с центром O и радиусом R. Пусть точка A — точка касания окружности и касательной. Проведем радиус OA от центра окружности к точке A.
Внутри треугольника OAB у нас есть две прямые: радиус OA и отрезок AB, которые пересекаются в точке A. Радиус OA является перпендикуляром к отрезку AB, так как радиус всегда перпендикулярен к касательной. Поскольку у нас есть две перпендикулярные прямые, образующие угол в точке A, эти прямые образуют прямой угол.
Таким образом, прямая AB является касательной к окружности в точке A. Это доказывает теорему о свойстве касательной.






