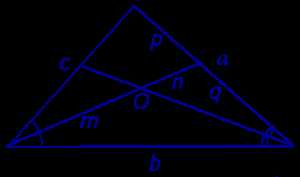
Что такое биссектриса треугольника и сколько их может быть? Биссектриса треугольника – это прямая, которая делит угол на два равных угла. Она начинается от вершины угла и пересекает противоположную сторону треугольника. Биссектрисы позволяют нам делить треугольник на два равных подтреугольника, а также определить место пересечения всех трех биссектрис, которое называется центром вписанной окружности. Количество биссектрис в треугольнике зависит от типа треугольника. В обычном треугольнике — всего три биссектрисы, которые треугольника в сумме образуют центр вписанной окружности. Однако, в прямоугольном треугольнике есть специальные биссектрисы, называемые высотами, которые делят прямый угол пополам.
Определение биссектрисы треугольника
В треугольнике может быть три биссектрисы, по одной для каждого угла. Каждая биссектриса исходит из вершины угла и делит противоположную ей сторону на две отрезка, пропорциональных соседним сторонам треугольника. Биссектрисы также пересекаются в одной точке, называемой центром вписанной окружности.
Зачем нам нужны биссектрисы треугольника? Во-первых, они помогают нам находить центр вписанной окружности, что имеет практическое применение в геометрии и инженерии. Во-вторых, биссектрисы могут служить как надежные опорные точки при построении и измерении углов.
Как определить биссектрису треугольника? Для этого можно использовать следующий алгоритм:
- Находим середину противоположной стороны треугольника.
- Проводим линию из вершины угла к середине противоположной стороны.
- Эта линия будет биссектрисой угла треугольника.
Биссектрисы треугольника имеют важное значение в геометрии и находят применение в различных областях науки и техники. Изучение и понимание их свойств помогут улучшить наши навыки в геометрии и решении сложных задач.
Как найти биссектрису треугольника?
Чтобы найти биссектрису треугольника, мы можем использовать следующий алгоритм:
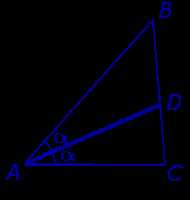
- Возьмите треугольник ABC и выберите один из его углов. Например, угол A.
- Проведите линию, исходящую из вершины A, которая будет делить угол A пополам.
- Пусть эта линия пересекает противоположную сторону BC в точке D.
- Теперь вы можете утверждать, что AD является биссектрисой угла ABC.
Доказательство этого факта можно найти с помощью геометрических построений и пропорциональности сторон треугольника.
Интересный факт: в треугольнике может быть три биссектрисы — по одной для каждого угла. Они могут пересекаться в одной точке, которая называется центром вписанной окружности треугольника.
| Тип треугольника | Количество биссектрис |
|---|---|
| Равносторонний | Три биссектрисы |
| Равнобедренный | Две биссектрисы |
| Разносторонний | Одна биссектриса |
Итак, нахождение биссектрисы треугольника является важным элементом геометрии. Она помогает нам разделять углы на равные части и определяет ряд других свойств треугольников. Помните, что биссектрисы могут быть найдены с использованием геометрических построений и пропорций сторон треугольника.
Свойства биссектрисы треугольника
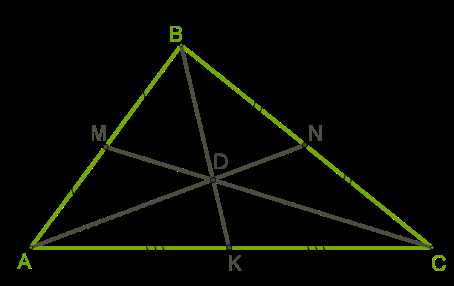
Вот некоторые из них:
- Любая биссектриса треугольника является перпендикуляром к соответствующей стороне треугольника.
- Точка пересечения биссектрис треугольника называется центром биссектрисы и находится в равном расстоянии от всех сторон треугольника.
- Биссектрисы треугольника могут быть использованы для нахождения площади треугольника с помощью формулы Герона, так как они делят сторону треугольника в соответствующих пропорциях.
- Произведение длин отрезков, на которые биссектрисы треугольника делят противоположные стороны, равно квадрату длины противоположной стороны. Это известно как теорема биссектрис треугольника.
Зная эти свойства, мы можем легко использовать биссектрисы для решения различных задач и нахождения неизвестных значений в треугольнике.
Таким образом, биссектрисы треугольника имеют большое значение в геометрии и предоставляют нам множество возможностей для изучения и решения задач, связанных с треугольником.
Сколько биссектрис может быть в треугольнике?
Давайте представим, что у нас есть треугольник ABC, и угол B разделен на два равных угла биссектрисой BD. Теперь у нас есть два новых угла — угол ABD и угол CBD. Больше углов нет и, соответственно, больше биссектрис тоже нет. Как вы можете видеть, треугольник всегда имеет только три угла и, следовательно, только три биссектрисы.
В общем случае, биссектрисы пересекаются внутри треугольника в одной точке, которая называется точкой биссектрис. Эта точка является одновременно центром вписанной окружности треугольника, которая касается всех трех сторон.
Итак, простой ответ на вопрос «Сколько биссектрис может быть в треугольнике?» — всегда ровно три.
Применение биссектрис треугольника
Биссектрисы треугольника играют важную роль в геометрии и находят свое применение как в учебных задачах, так и в реальной жизни. Они позволяют нам изучать и анализировать свойства треугольника, а также решать различные задачи, связанные с треугольниками.
Во-первых, биссектрисы треугольника могут быть использованы для нахождения площади треугольника. Представляя собой прямые линии, которые делят углы треугольника пополам, биссектрисы позволяют нам разделить треугольник на две равные по площади части. А затем, зная формулу площади треугольника (S = 0.5 * основание * высота), мы можем легко найти площадь треугольника.
Кроме того, биссектрисы треугольника помогают нам находить длины его сторон. При использовании теоремы биссектрисы треугольника, мы можем найти длины сторон на основе длин других сторон и длин биссектрис. Это может быть полезно при решении задач на построение треугольников или при нахождении неизвестных сторон в известном треугольнике.
Кроме учебных задач, биссектрисы треугольника имеют применение и в реальной жизни. Например, в архитектуре и дизайне, биссектрисы могут использоваться для создания симметричных и гармоничных форм. Они также могут быть использованы в решении практических задач, связанных с треугольниками, например, при строительстве или изготовлении различных конструкций.
Таким образом, биссектрисы треугольника являются важным инструментом для изучения и анализа треугольников, а также для решения задач, связанных с ними. Они находят широкое применение как в учебных задачах, так и в реальной жизни, и помогают нам лучше понять и использовать свойства треугольников в различных областях.






