
Арктангенс (tangent-1) — это обратная функция к тангенсу (tg). То есть, арктангенс от числа x — это угол, тангенс которого равен числу x.
Для определения значения арктангенса от числа 3, нам необходимо найти угол, тангенс которого равен 3.
Однако, стоит отметить, что арктангенс функция не определена для всех значений тангенса, а только в определенном диапазоне.
Точное значение арктангенса от 3 зависит от заданного интервала.
Определение арктангенса
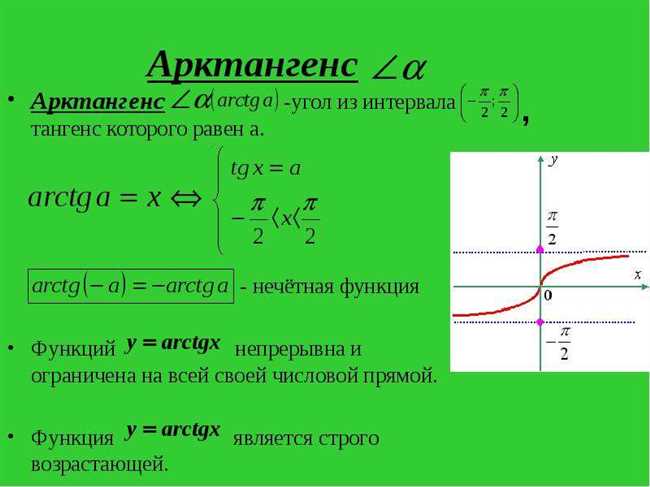
Арктангенс относится к классу тригонометрических функций, которые используются в математике и физике для решения различных задач. Он помогает нам находить значения углов и расстояний в пространстве.
Арктангенс может быть выражен в радианах или градусах. Обычно, если ничего не указано, считается, что арктангенс выражен в радианах.
Арктангенс имеет свойства и ограничения, которые стоит учесть при его использовании:
- В отличие от тангенса, арктангенс имеет ограниченную область значений. Принимает значения от -π/2 до π/2 по умолчанию или от -90° до 90° в градусах.
- Может принимать только одно значения для каждого заданного аргумента. Например, арктангенс от 1 равен π/4 (или 45°), а арктангенс от -1 равен -π/4 (или -45°).
Важно помнить, что значения арктангенса отличаются в разных квадрантах. Например, арктангенс от 1 будет иметь разное значение в первом и третьем квадрантах, так как тангенс изменяется в этих областях.
Арктангенс широко применяется в геометрии, физике, инженерии и других областях науки. Он помогает решать задачи, связанные с треугольниками, тригонометрическими уравнениями и моделированием физических явлений.
Тригонометрический круг и его особенности
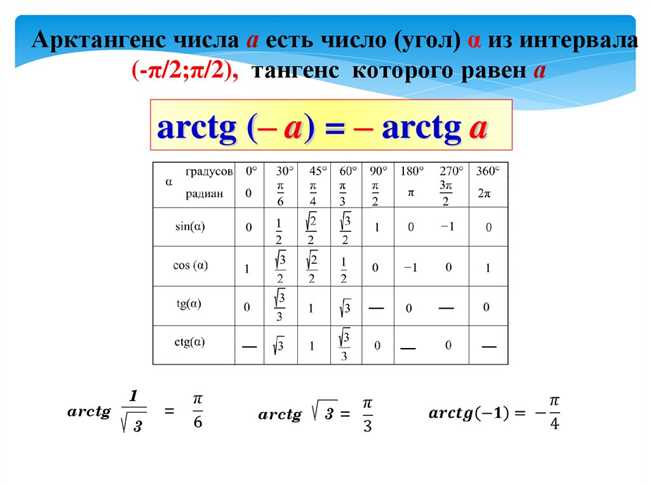
Всего в тригонометрическом круге 360°, что соответствует 2π радиан. Этот круг помогает нам понять и визуализировать связь между углами и значением тригонометрических функций.
Основные особенности тригонометрического круга:
- Начальная точка находится в верхней части круга, которая соответствует углу 0° или 0 радиан.
- Положительное направление движения по кругу против часовой стрелки.
- Хорда, соединяющая начальную точку и точку на круге, определяет угол, измеряемый в радианах или градусах.
- Круг поделен на четыре квадранта, каждый из которых имеет свои особенности. Каждый квадрант соответствует определенному диапазону углов и значениям тригонометрических функций.
Тригонометрический круг является основой для понимания и использования тригонометрических функций, таких как синус, косинус, тангенс, котангенс, секанс и косеканс. Каждая из этих функций имеет свои особенности и связь с углами на тригонометрическом круге.
Теперь, вернемся к вопросу «Чему равен арктангенс от 3?» На тригонометрическом круге арктангенс от 3 соответствует углу, тангенс которого равен 3. Ответ можно получить, используя свойство обратной функции тангенса. То есть, мы ищем угол, тангенс которого равен 3. В данном случае, это примерно 71.57° или примерно 1.24 радиана.
Арктангенс от 3

Тангенс — это тригонометрическая функция, определенная как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Она может принимать различные значения в зависимости от угла, на который она применяется.
Тангенс 3 равен 3. Это означает, что прилежащий катет в треугольнике имеет длину 3, а противолежащий катет имеет длину 1. Треугольник, у которого такие пропорции сторон, называется тангенсальным треугольником для угла 3.
Итак, арктангенс от 3 равен углу, тангенс которого равен 3. Чтобы найти его значение, можно воспользоваться табличными или калькуляторными значениями функции арктангенс. Например, арктангенс от 3 составляет примерно 71.57 градусов или 1.25 радиан.
Знание арктангенса от 3 может быть полезно в решении геометрических и тригонометрических задач, а также в науках, где применяются функции тангенса и обратных к ним функций. Например, в физике и инженерии может потребоваться рассчитать угол, для которого тангенс равен определенному значению.
Надеюсь, этот краткий обзор помог вам понять, что такое арктангенс от 3 и как его использовать. Если у вас возникли ещё вопросы, не стесняйтесь задавать их!
Применение арктангенса в математике и физике
В математике арктангенс используется, например, для нахождения углов в треугольниках. С помощью этой функции можно определить угол между двумя сторонами треугольника, зная их длины. Также арктангенс применяется в анализе функций и решении уравнений, где тангенс является одним из элементарных функций.
В физике арктангенс также играет важную роль. Он используется для моделирования законов движения тела с учетом силы притяжения, например, при расчетах траектории движения снаряда или спутника. Знание арктангенса позволяет определить угол броска, необходимый для достижения определенной дальности полета.
Использование арктангенса в математике и физике позволяет решать сложные задачи, связанные с тригонометрией и геометрией. Эта функция является неотъемлемым инструментом для профессионалов в этих областях и позволяет анализировать и предсказывать множество явлений и процессов в природе.






