
Арктангенс бесконечности — это математическая формула, которая определяет значение арктангенса для аргумента, стремящегося к бесконечности. Арктангенс — это обратная функция тангенса, которая показывает угол, для которого тангенс равен данному числу. Когда аргумент стремится к бесконечности, значение арктангенса также стремится к определенному пределу. Арктангенс бесконечности может быть выражен в виде численного значения, используя различные методы и приближения. Эта формула и связанные с ней свойства широко используются в различных областях науки и инженерии, таких как физика, электротехника и компьютерная графика. Понимание арктангенса бесконечности является важным для решения различных математических и инженерных задач, связанных с бесконечными пределами и углами.
Описание арктангенса бесконечности
Дорогой читатель, разве не удивительно, что мы можем говорить о математике, используя такие величественные слова, как «бесконечность»? И это не просто философское понятие, а математический термин, который имеет свое определение и значение. Сегодня мы с тобой отправимся в увлекательное путешествие в мир арктангенса бесконечности и его свойств.
Арктангенс — это функция, обратная к тангенсу. Если ты знаком с тангенсом, то знаешь, что он выражает отношение противоположной и ближайшей катетов в прямоугольном треугольнике. Но что произойдет, когда этот треугольник будет стремиться к бесконечности?
Значение арктангенса бесконечности
Когда мы говорим о значении арктангенса бесконечности, мы имеем в виду предел этой функции, когда аргумент функции стремится к бесконечности. Арктангенс бесконечности определяется как угол, при котором тангенс этого угла равен бесконечности.
Но, возможно, ты задаешься вопросом: каким может быть тангенс угла, который равен бесконечности? Это хороший вопрос! В этом случае, мы можем сказать, что арктангенс бесконечности также равен бесконечности.
Мы можем представить себе ситуацию, когда тригонометрические функции применяются к углам, которые не имеют конечного значения. Изучение таких функций позволяет нам расширить наши знания о математике и понять ее глубокие связи с нашим миром.
Свойства арктангенса бесконечности
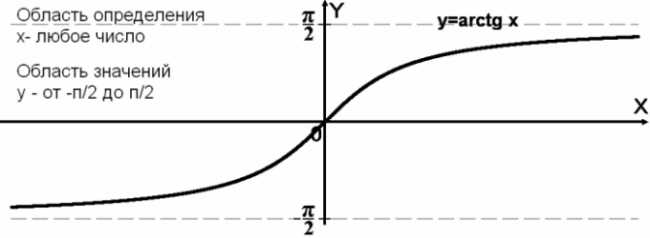
Теперь, когда мы разобрались с определением и значением арктангенса бесконечности, давайте рассмотрим некоторые его свойства, чтобы лучше понять эту интересную математическую функцию.
- Арктангенс бесконечности всегда равен бесконечному углу, независимо от его аргумента.
- Он может быть представлен как асимптотическая функция, которая стремится к бесконечности при приближении аргумента к бесконечности.
- Его значения могут быть выражены в радианах или градусах, в зависимости от системы измерения углов.
Важно отметить, что арктангенс бесконечности является лишь одним из множества трехгранных углов, а его значение и свойства могут иметь глубокие математические и физические значения.
Дорогой читатель, теперь ты знаешь описания и значение арктангенса бесконечности. Я надеюсь, что ты найдешь интерес в этой удивительной области математики и бесконечности и сможешь применить эти знания в своей жизни.
Что такое арктангенс бесконечности?
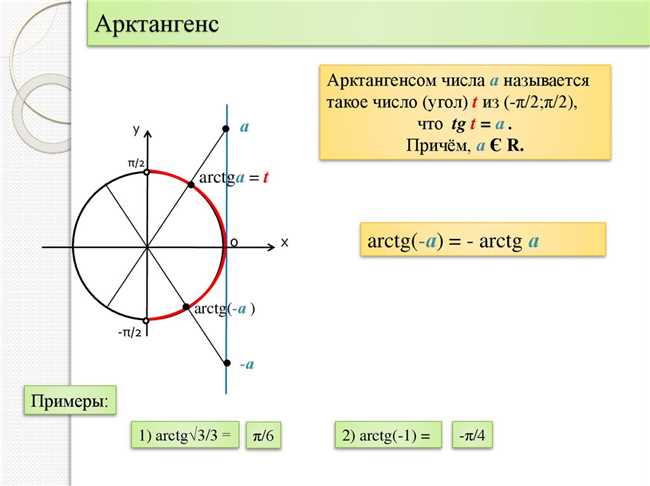
Для лучшего понимания, давайте вспомним, что такое тангенс. Тангенс угла рассчитывается как отношение противоположной стороны к прилегающей стороне в прямоугольном треугольнике. Таким образом, тангенс угла может быть любым числом, включая бесконечность.
Арктангенс бесконечности определяет угол, при котором тангенс достигает бесконечности. Это полезно в различных областях науки и инженерии, где необходимо рассчитать такие углы и использовать их в дальнейших вычислениях.
Например, в физике арктангенс бесконечности может использоваться для расчета угла броска тела, которое движется с бесконечно большой начальной скоростью. В экономике это может быть полезно для определения точки безубыточности или того момента, когда прибыль достигает бесконечности.
Арктангенс бесконечности также имеет связь с другими тригонометрическими функциями, такими как арксинус и арккосинус. Вместе они образуют семейство функций, которые помогают в решении различных математических задач.
Формула для вычисления арктангенса бесконечности
Формула для вычисления арктангенса бесконечности имеет вид:
- Если значение бесконечности положительное, то арктангенс равен π/2.
- Если значение бесконечности отрицательное, то арктангенс равен -π/2.
Таким образом, арктангенс бесконечности может принимать только два значения: π/2 или -π/2. Это связано с тем, что при стремлении значения тангенса к бесконечности, угол также стремится к π/2 или -π/2, что соответствует горизонтальной прямой на графике тангенса.
Есть ли у тебя вопросы по этой теме? Что еще тебя интересует о формуле для вычисления арктангенса бесконечности? Я с радостью помогу тебе разобраться в этой математической теме!
Значение арктангенса бесконечности
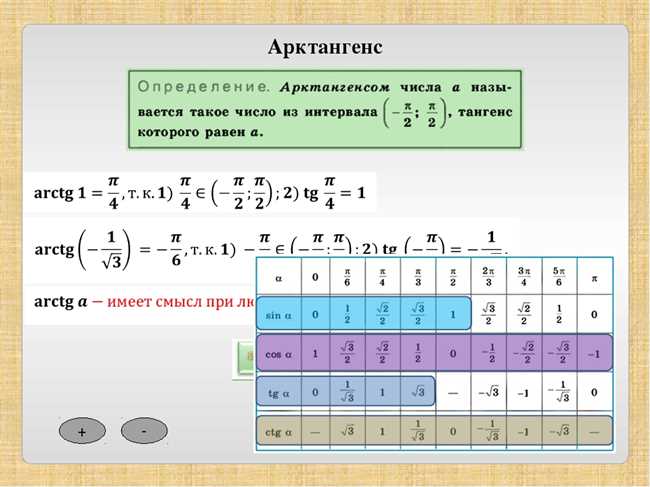
Арктангенс — это обратная функция тангенса и она определена для всех реальных чисел, кроме точек, где тангенс равен бесконечности. Но что происходит, когда аргумент функции арктангенса становится бесконечным?
Когда аргумент функции арктангенса стремится к бесконечности, значение функции также стремится к определенному числу. Это число является математической константой и обозначается как π/2 или 1.570796327…
- Значение арктангенса бесконечности равно π/2 или 1.570796327…
- Математические инструменты, такие как калькуляторы и компьютерные программы, используют приближенное значение этой константы для удобства расчетов.
- Значение π/2 является частью общей формулы арктангенса и позволяет определить другие значения функции.
Важно отметить, что аргумент функции арктангенса, стремящийся к бесконечности, может быть представлен в разных формах, таких как положительная или отрицательная бесконечность, а также бесконечность, приближающаяся к нулю или другому числу. Но во всех этих случаях значение арктангенса будет равно π/2.
Знание значения арктангенса бесконечности играет важную роль в различных областях науки и техники, таких как физика, инженерия и информатика. Оно помогает решать сложные задачи и моделировать поведение систем при очень больших значениях аргумента.
Таким образом, значением арктангенса бесконечности является π/2 (или 1.570796327…), и оно играет важную роль в математике и ее приложениях.
Свойства арктангенса бесконечности
Одно из основных свойств арктангенса бесконечности состоит в том, что он принимает значение пи/2. Это означает, что при стремлении аргумента к бесконечности, арктангенс будет стремиться к углу, равному 90 градусам или пи/2 радиан.
Также стоит отметить, что арктангенс бесконечности имеет некоторые другие свойства, которые можно выразить следующим образом:
- arctan(inf) = pi/2
- arctan(-inf) = -pi/2
- arctan(inf) = arctan(-inf)
Эти свойства позволяют использовать арктангенс бесконечности в математических и физических расчетах для решения различных задач.






