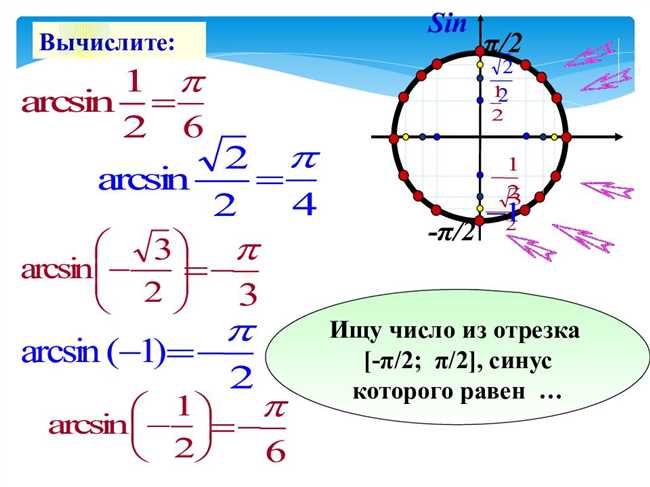
Арксинус – математическая функция, обратная к синусу. В основе арксинуса лежит понятие обратной функции, то есть функции, которая переводит значение, полученное при выполнении какой-либо операции, обратно в исходное значение. Арксинус обозначается как arcsin(x) и определен на интервале [-1, 1]. Результатом выполнения арксинуса является угол, синус которого равен аргументу функции. Эта функция активно используется в различных областях, таких как геометрия, физика, статистика и программирование. Например, она может быть применена в расчетах для нахождения угла между двумя векторами или в решении геометрических задач. Изучение и понимание арксинуса помогает углубить знания в области математики и использовать его в практических расчетах.
Определение арксинуса

Арксинус обозначается как arcsin или sin-1. Например, если sin(α) = 0.5, то arcsin(0.5) = α.
Значения арксинуса находятся в пределах от -π/2 до π/2 радиан (от -90° до 90°). Они могут быть выражены в радианах или градусах.
Арксинус является многозначной функцией, то есть для одного значения синуса существует бесконечное количество углов, у которых синус равен этому значению. Обычно выбирается одно из таких значений в определенном интервале для облегчения вычислений.
Арксинус имеет много практических применений. Например, он может использоваться для решения треугольников, нахождения невозможных углов в прямоугольных треугольниках, определения точных значений углов, а также в различных областях физики, инженерии и компьютерной графики.
Вот таблица значений арксинуса для некоторых общих значений синуса:
| Синус | Арксинус |
|---|---|
| 0 | 0 |
| 1/2 | π/6 |
| √2/2 | π/4 |
| 1 | π/2 |
Надеюсь, это определение поможет вам лучше понять, что такое арксинус и как его использовать.
Свойства арксинуса
У арксинуса есть несколько свойств, которые помогают в его применении в различных областях.
1. Область значений и определенность
Арксинус определен на интервале [-1, 1], так как значения синуса ограничены этим интервалом. Область значений арксинуса — это интервал [-π/2, π/2].
2. Симметрия
Арксинус обладает симметричными свойствами относительно оси y=-x и оси y=x. Это означает, что для любого значения x фунцкии arcsin(x), справедливы равенства arcsin(-x) = -arcsin(x) и arcsin(x) = π — arcsin(-x).
3. Ограничение на основную четверть
В основной четверти, где значение арксинуса находится в диапазоне от -π/2 до π/2, функция арксинус монотонно возрастает с ростом значения. Это означает, что при увеличении значения x, значение arcsin(x) также увеличивается.
4. Отношение к синусу
Синус и арксинус являются взаимно обратными функциями: sin(arcsin(x)) = x для всех x, принадлежащих области определения arcsin(x). Это делает арксинус полезным инструментом для решения уравнений и нахождения неизвестных углов, основанных на заданном отношении синуса.
Таким образом, арксинус имеет несколько свойств, которые делают его полезным инструментом в математике, физике, инженерии и других областях. Он позволяет нам находить углы, основанные на заданных отношениях синуса, и решать уравнения, связанные с синусом.
Применение арксинуса
1. Решение уравнений и систем уравнений
Арксинус позволяет решать уравнения, в которых синус является неизвестной. Он обратно связывает значения синуса с углами, что позволяет найти значения углов, удовлетворяющих определенным условиям.
2. Тригонометрия и геометрия
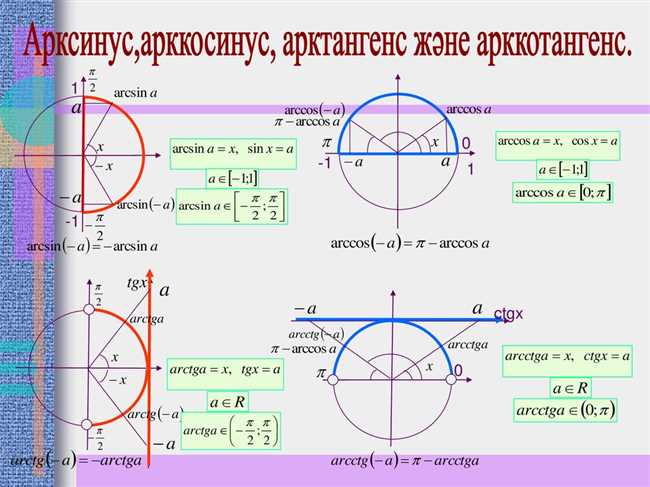
Арксинус используется для нахождения углов исходя из значений синуса. Он позволяет вычислять углы в треугольниках и других геометрических фигурах, основываясь на соответствующих значений синуса.
3. Компьютерные приложения и моделирование
Арксинус широко используется в компьютерных приложениях и моделировании для обработки данных, вычислений и построения графиков. Например, он может быть использован для создания графиков синусоиды или для вычисления углов поворота объектов в трехмерном пространстве.
Использование арксинуса в различных областях позволяет нам лучше понять и моделировать мир вокруг нас, а также решать разнообразные математические и физические задачи. Эта функция открывает перед нами много возможностей в науке и технике.






